Published On:Wednesday, 14 December 2011
Posted by Muhammad Atif Saeed
Second-Degree Equations and Inequalities
Second-degree equations involve at least one variable that is squared, or raised to a power of two. One of the most well-known second-degree equations is the quadratic 
where a, b, and c are constants and a is not equal 0. Second-degree equations have two possible solutions: 
and 
The graph of a second-degree equation produces a parabola. The solutions to the equation represent where the parabola crosses the x-axis. The general form of second-degree inequalities is
. Solving inequalities involves finding all possible values of the variable that will make the inequality true.
where a, b, and c are constants and a is not equal 0. Second-degree equations have two possible solutions: and The graph of a second-degree equation produces a parabola. The solutions to the equation represent where the parabola crosses the x-axis. The general form of second-degree inequalities is
. Solving inequalities involves finding all possible values of the variable that will make the inequality true. QUADRATIC IS ANOTHER NAME for a polynomial of the 2nd degree. 2 is the highest exponent.
We begin with the method of factoring. In the following Topic, we will present Completing the square and The quadratic formula.
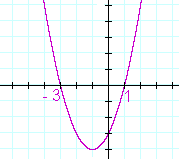
Example 1. Solution by factoring. f(x) = x² −2x −3. Find the roots of f(x), and sketch the graph of y = f(x).
The y-intercept is the constant term, −3.
In every polynomial the y-intercept is the constant term, because the constant term is the value of y when x = 0.
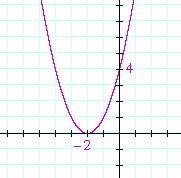
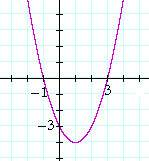
Example 2. A double root. f(x) = x² −10x + 25. Find the roots of
f(x), and sketch the graph of y = f(x).
f(x), and sketch the graph of y = f(x).
At a double root, the graph does not cross the x-axis. It just touches it.
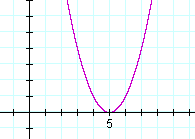
A double root occurs when the quadratic is a perfect square trinomial: x² ±2ax + a²; that is, when the quadratic is the square of a binomial: (x ± a)².
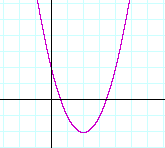
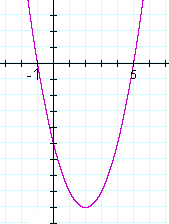
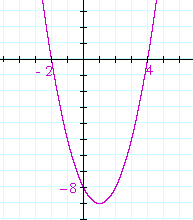
Example 3. How many real roots, i.e. roots that are real numbers, has the quadratic of each graph?
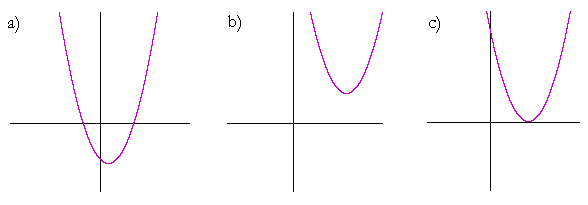
Answer. Graph a) has two real roots. It has two x-intercepts.
Graph b) has no real roots. It has no x-intercepts. Both roots are complex.
Graph c) has two real roots. But they are a double root.
Problem 4. A quadratic has the following roots. Write each quadratic as a product of linear factors.
a) 3, 4 (x − 3)(x − 4)
b) −3, −4 (x + 3)(x + 4)
c) −r, s (x + r)(x − s)
d) 3 +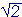 
, 3 − (x − 3 − 
)(x −3 + )
, 3 − 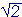(x − 3 − 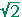)(x −3 + 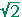)| r + s | = | −b, |
| rs | = | c. |
| (x − r)(x − s) | = | x² − rx − sx + rs |
| = | x² − (r + s)x + rs. | |
Solution. The sum of the roots is 4. Their product is the Difference of two squares: 2² − (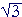
)² = 4 − 3 = 1.
)² = 4 − 3 = 1.The quadratic therefore is x² − 4x + 1.
Example 7. Construct the quadratic whose roots are 2 + 3i, 2 − 3i, where i is the complex unit.
Solution. The sum of the roots is 4. The product again is the Difference of Two Squares: 4 − 9i² = 4 + 9 = 13.
The quadratic with those roots is x² − 4x + 13.
Problem 5. Construct the quadratic whose roots are −3, 4.
The sum of the roots is 1. Their product is −12. Therefore, the quadratic is x² − x − 12.
Problem 6. Construct the quadratic whose roots are 3 + 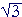, 3 − .
, 3 − 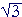. The sum of the roots is 6. Their product is 9 − 3 = 6.
Therefore, the quadratic is x² − 6x + 6.
Therefore, the quadratic is x² − 6x + 6.
Problem 7. Construct the quadratic whose roots are 2 + i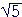
, 2 − i.
, 2 − i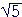. The sum of the roots is 4. Their product is 4 − (i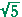
)² = 4 + 5 = 9.
Therefore, the quadratic is x² − 4x + 9.
)² = 4 + 5 = 9.Therefore, the quadratic is x² − 4x + 9.
*
More generally, for any coefficient of x², that is, if the quadratic is
ax² + bx + c,
and the roots are r and s, then
| r + s | = | − | b a | , |
| rs | = | c a | . | |
When a = 1, we have the theorem above.
