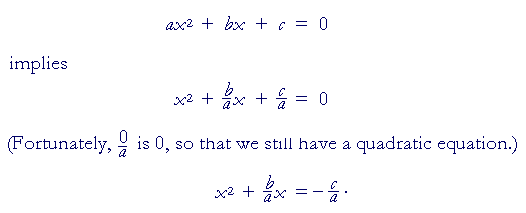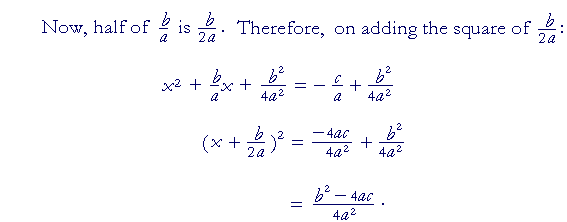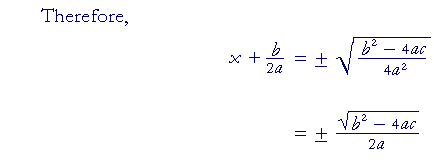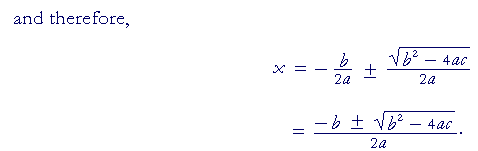Published On:Wednesday, 14 December 2011
Posted by Muhammad Atif Saeed
COMPLETING THE SQUARE
COMPLETING THE SQUARE
IF WE TRY TO SOLVE this quadratic equation by factoring
x² + 6x + 2 = 0
we cannot. Therefore, we use a technique called completing the square. That means to make the quadratic into a perfect square trinomial, i.e. the form a² + 2ab + b² = (a + b)².
The technique is valid only when 1 is the coefficient of x².1) Transpose the constant term to the right:
x² + 6x = −2
2) Add a square number to both sides. Add the square of half the coefficient of x. In this case, add the square of 3:x² + 6x + 9 = −2 + 9
The left-hand side is now the perfect square of (x + 3).
(x + 3)² = 7.
3 is half of the coefficient 6.
This equation has the form
| a² | = | b | |
| which implies | |||
| a | = | ± | |
| Therefore, | |||
| x + 3 | = | ± | |
| x | = | −3 ± | |
That is, the solutions to
x² + 6x + 2 = 0
are the conjugate pair,
−3 +  , −3 −
, −3 −  .
.
We can check this. The sum of those roots is −6, which is the negative of the coefficient of x. And the product of the roots is
(−3)² − ( )² = 9 − 7 = 2,
)² = 9 − 7 = 2,
which is the constant term. Thus both conditions on the roots are satisfied. These are the two roots of the quadratic.
| x² − 2x | = | 2 |
| x² − 2x + 1 | = | 2 + 1 |
| (x − 1)² | = | 3 |
| x − 1 | = | ± |
| x | = | 1 ± |
| number b is | b 2 | . Half of 5 is | 5 2 | . Half of | p q | is | p 2q | . | ||||