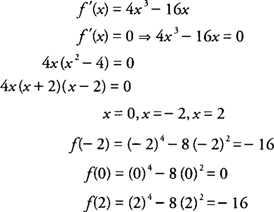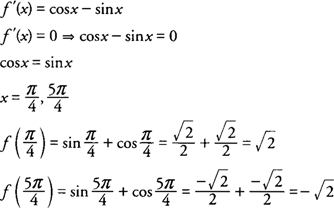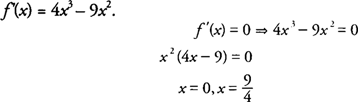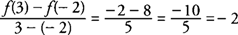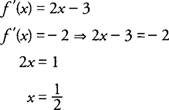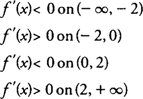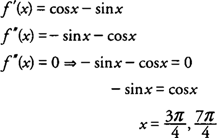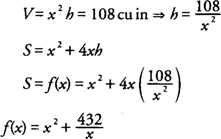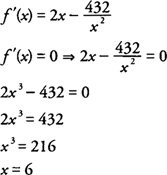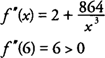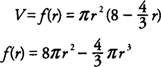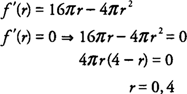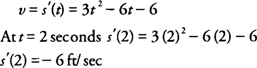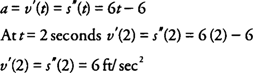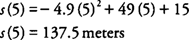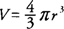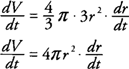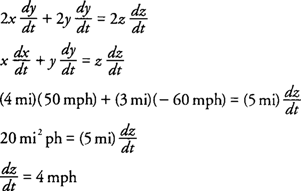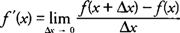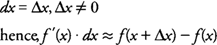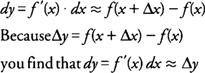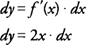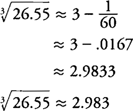Tangent and Normal Lines
The derivative of a function has many applications to problems in calculus. It may be used in curve sketching; solving maximum and minimum problems; solving distance; velocity, and acceleration problems; solving related rate problems; and approximating function values.
The derivative of a function at a point is the slope of the tangent line at this point. The
normal line is defined as the line that is perpendicular to the tangent line at the point of tangency. Because the slopes of perpendicular lines (neither of which is vertical) are negative reciprocals of one another, the slope of the normal line to the graph of
f(x) is −1/
f′(x).
Example 1: Find the equation of the tangent line to the graph of
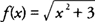
at the point (−1,2).
At the point (−1,2),
f′(−1)=−½ and the equation of the line is
Example 2: Find the equation of the normal line to the graph of
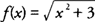
at the point (−1, 2).
From Example 1, you find that
f′(−1)=−½ and the slope of the normal line is −1/
f′(−1) = 2; hence, the equation of the normal line at the point (−1,2) is
Critical Points
Points on the graph of a function where the derivative is zero or the derivative does not exist are important to consider in many application problems of the derivative. The point (
x, f(x)) is called a
critical point of
f(x) if
x is in the domain of the function and either
f′(x) = 0 or
f′(x) does not exist. The geometric interpretation of what is taking place at a critical point is that the tangent line is either horizontal, vertical, or does not exist at that point on the curve.
Example 1: Find all critical points of
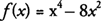
.
Because
f(x) is a polynomial function, its domain is all real numbers.
hence, the critical points of
f(x) are (−2,−16), (0,0), and (2,−16).
Example 2: Find all critical points of
f(x)= sin
x + cos
x on [0,2π].
The domain of
f(x) is restricted to the closed interval [0,2π].
hence, the critical points of
f(x) are
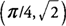
and
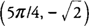
Extreme Value Theorem
An important application of critical points is in determining possible maximum and minimum values of a function on certain intervals. The
Extreme Value Theorem guarantees both a maximum and minimum value for a function under certain conditions. It states the following:
- If a function f(x) is continuous on a closed interval [ a, b], then f(x) has both a maximum and minimum value on [ a, b].
The procedure for applying the Extreme Value Theorem is to first establish that the function is continuous on the closed interval. The next step is to determine all critical points in the given interval and evaluate the function at these critical points and at the endpoints of the interval. The largest function value from the previous step is the maximum value, and the smallest function value is the minimum value of the function on the given interval.
Example 1: Find the maximum and minimum values of
f(x) = sin
x + cos
x on [0, 2π].
The function is continuous on [0,2π], and the critcal points are
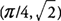
and
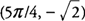
. The function values at the end points of the interval are
f(0) = 1 and
f(2π)=1; hence, the maximum function value of
f(x) is
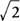
at
x=π/4, and the minimum function value of
f(x) is −
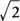
at
x = 5π/4.
Note that for this example the maximum and minimum both occur at critical points of the function.
Example 2: Find the maximum and minimum values of
f(x)=
x4−3
x3−1 on [−2,2].
The function is continuous on [−2,2], and its derivative is
f′(x)=4
x3−9
x2.
Because
x=9/4 is not in the interval [−2,2], the only critical point occurs at
x = 0 which is (0,−1). The function values at the endpoints of the interval are
f(2)=−9 and
f(−2)=39; hence, the maximum function value 39 at
x = −2, and the minimum function value is −9 at
x = 2. Note the importance of the closed interval in determining which values to consider for critical points.
Mean Value Theorem
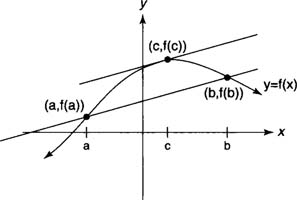
The
Mean Value Theorem establishes a relationship between the slope of a tangent line to a curve and the secant line through points on a curve at the endpoints of an interval. The theorem is stated as follows.
If a function
f(x) is continuous on a closed interval [a,b] and differentiable on an open interval (a,b), then at least one number c ∈ (a,b) exists such that
|
|
|
| Figure 1 | The Mean Value Theorem. |
|
|
Geometrically, this means that the slope of the tangent line will be equal to the slope of the secant line through (a,f(a)) and (b,f(b)) for at least one point on the curve between the two endpoints. Note that for the special case where f(a) = f(b), the theorem guarantees at least one critical point, where f(c) = 0 on the open interval ( a, b).
Example 1: Verify the conclusion of the Mean Value Theorem for f(x)= x2−3 x−2 on [−2,3].
The function is continuous on [−2,3] and differentiable on (−2,3). The slope of the secant line through the endpoint values is
The slope of the tangent line is
Because ½ ∈ [−2,3], the
c value referred to in the conclusion of the Mean Value Theorem is
c = ½
Increasing/Decreasing Functions
The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain. If
f′(x) > 0 at each point in an interval I, then the function is said to be increasing on I.
f′(x) < 0 at each point in an interval I, then the function is said to be
decreasing on I. Because the derivative is zero or does not exist only at critical points of the function, it must be positive or negative at all other points where the function exists.
In determining intervals where a function is increasing or decreasing, you first find domain values where all critical points will occur; then, test all intervals in the domain of the function to the left and to the right of these values to determine if the derivative is positive or negative. If
f′(x) > 0, then
f is increasing on the interval, and if
f′(x) < 0, then
f is decreasing on the interval. This and other information may be used to show a reasonably accurate sketch of the graph of the function.
Example 1: For
f(x) =
x4 − 8
x2 determine all intervals where
f is increasing or decreasing.
The domain of
f(x) is all real numbers, and its critical points occur at
x = −2, 0, and 2. Testing all intervals to the left and right of these values for
f′(x) = 4
x3 − 16
x, you find that
hence,
f is increasing on (−2,0) and (2,+ ∞) and decreasing on (−∞, −2) and (0,2).
Example 2: For
f(x) = sin
x + cos
x on [0,2π], determine all intervals where
f is increasing or decreasing.
The domain of
f(x) is restricted to the closed interval [0,2π], and its critical points occur at π/4 and 5π/4. Testing all intervals to the left and right of these values for
f′(x) = cos
x − sin
x, you find that
hence,
f is increasing on [0, π/4](5π/4, 2π) and decreasing on (π/4, 5π/4).
First Derivative Test for Local Extrema
If the derivative of a function changes sign around a critical point, the function is said to have a
local (relative) extremum at that point. If the derivative changes from positive (increasing function) to negative (decreasing function), the function has a
local (relative) maximum at the critical point. If, however, the derivative changes from negative (decreasing function) to positive (increasing function), the function has a
local (relative) minimum at the critical point. When this technique is used to determine local maximum or minimum function values, it is called the
First Derivative Test for Local Extrema. Note that there is no guarantee that the derivative will change signs, and therefore, it is essential to test each interval around a critical point.
Example 1: If
f(x) =
x4 − 8
x2, determine all local extrema for the function.
f(x) has critical points at
x = −2, 0, 2. Because
f'(x) changes from negative to positive around −2 and 2,
f has a local minimum at (−2,−16) and (2,−16). Also,
f'(x) changes from positive to negative around 0, and hence,
f has a local maximum at (0,0).
Example 2: If
f(x) = sin
x + cos
x on [0, 2π], determine all local extrema for the function.
f(x) has critical points at
x = π/4 and 5π/4. Because
f′(x) changes from positive to negative around π/4,
f has a local maximum at
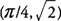
. Also
f′(x) changes from negative to positive around 5π/4, and hence,
f has a local minimum at
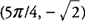
Second Derivative Test for Local Extrema
The second derivative may be used to determine local extrema of a function under certain conditions. If a function has a critical point for which
f′(x) = 0 and the second derivative is positive at this point, then
f has a local minimum here. If, however, the function has a critical point for which
f′(x) = 0 and the second derivative is negative at this point, then
f has local maximum here. This technique is called
Second Derivative Test for Local Extrema.
Three possible situations could occur that would rule out the use of the Second Derivative Test for Local Extrema:
Under any of these conditions, the First Derivative Test would have to be used to determine any local extrema. Another drawback to the Second Derivative Test is that for some functions, the second derivative is difficult or tedious to find. As with the previous situations, revert back to the First Derivative Test to determine any local extrema.
Example 1: Find any local extrema of
f(x) =
x4 − 8
x2 using the Second Derivative Test.
f′(x) = 0 at
x = −2, 0, and 2. Because
f″(x) = 12
x2 −16, you find that
f″(−2) = 32 > 0, and
f has a local minimum at (−2,−16);
f″(2) = 32 > 0, and
f has local maximum at (0,0); and
f″(2) = 32 > 0, and
f has a local minimum (2,−16).
Example 2: Find any local extrema of
f(x) = sin
x + cos
x on [0,2π] using the Second Derivative Test.
f′(x) = 0 at
x = π/4 and 5π/4. Because
f″(x) = −sin
x −cos
x, you find that
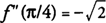
and
f has a local maximum at
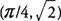
. Also,
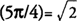
. and
f has a local minimum at
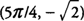
.
Concavity and Points of Inflection
The second derivative of a function may also be used to determine the general shape of its graph on selected intervals. A function is said to be
concave upward on an interval if
f″(x) > 0 at each point in the interval and
concave downward on an interval if
f″(x) < 0 at each point in the interval. If a function changes from concave upward to concave downward or vice versa around a point, it is called a
point of inflection of the function.
In determining intervals where a function is concave upward or concave downward, you first find domain values where
f″(x) = 0 or
f″(x) does not exist. Then test all intervals around these values in the second derivative of the function. If
f″(x) changes sign, then (
x, f(x)) is a point of inflection of the function. As with the First Derivative Test for Local Extrema, there is no guarantee that the second derivative will change signs, and therefore, it is essential to test each interval around the values for which
f″(x) = 0 or does not exist.
Geometrically, a function is concave upward on an interval if its graph behaves like a portion of a parabola that opens upward. Likewise, a function that is concave downward on an interval looks like a portion of a parabola that opens downward. If the graph of a function is linear on some interval in its domain, its second derivative will be zero, and it is said to have no concavity on that interval.
Example 1: Determine the concavity of
f(x) =
x3 − 6
x2 −12
x + 2 and identify any points of inflection of
f(x).
Because
f(x) is a polynomial function, its domain is all real numbers.
Testing the intervals to the left and right of
x = 2 for
f″(x) = 6
x −12, you find that
hence,
f is concave downward on (−∞,2) and concave upward on (2,+ ∞), and function has a point of inflection at (2,−38)
Example 2: Determine the concavity of
f(x) = sin
x + cos
x on [0,2π] and identify any points of inflection of
f(x).
The domain of
f(x) is restricted to the closed interval [0,2π].
Testing all intervals to the left and right of these values for
f″(x) = −sin
x − cos
x, you find that
hence,
f is concave downward on [0,3π/4] and [7π/4,2π] and concave upward on (3π/4,7π/4) and has points of inflection at (3π/4,0) and (7π/4,0).
Maximum/Minimum Problems
Many application problems in calculus involve functions for which you want to find maximum or minimum values. The restrictions stated or implied for such functions will determine the domain from which you must work. The function, together with its domain, will suggest which technique is appropriate to use in determining a maximum or minimum value—the Extreme Value Theorem, the First Derivative Test, or the Second Derivative Test.
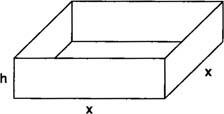
Example 1: A rectangular box with a square base and no top is to have a volume of 108 cubic inches. Find the dimensions for the box that require the least amount of material.
The function that is to be minimized is the surface area (
S) while the volume (
V) remains fixed at 108 cubic inches (Figure
1 )
|
|
|
| Figure 1 | The open-topped box for Example 1. |
|
|
. Letting x = length of the square base and h = height of the box, you find that
with the domain of f(x) = (0,+∞) because x represents a length.
hence, a critical point occurs when
x = 6. Using the Second Derivative Test:
and
f has a local minimum at
x = 6; hence, the dimensions of the box that require the least amount of material are a length and width of 6 inches and a height of 3 inches.
Example 2: A right circular cylinder is inscribed in a right circular cone so that the center lines of the cylinder and the cone coincide. The cone has 8 cm and radius 6 cm. Find the maximum volume possible for the inscribed cylinder.
The function that is to be maximized is the volume ( V) of a cylinder inscribed in a cone with height 8 cm and radius 6 cm (Figure 2 )
|
|
|
| Figure 2 | A cross section of the cone and cylinder for Example 2. |
|
|
. Letting r = radius of the cylinder and h = height of the cylinder and applying similar triangles, you find that
Because V = π r2 h and h = 8 −(4/3) r, you find that
with the domain of
f(r) = [0,6] because
r represents the radius of the cylinder, which cannot be greater that the radius of the cone.
Because
f(r) is continuous on [0,6], use the Extreme Value Theorem and evaluate the function at its critical points and its endpoints; hence,
hence, the maximum volume is 128π/3 cm
3, which will occur when the radius of the cylinder is 4 cm and its height is 8/3 cm.
Distance, Velocity, and Acceleration
As previously mentioned, the derivative of a function representing the position of a particle along a line at time
t is the instantaneous velocity at that time. The derivative of the velocity, which is the second derivative of the position function, represents the
instantaneous acceleration of the particle at time
t.
If
y =
s(t) represents the position function, then
v =
s′(t) represents the instantaneous velocity, and
a =
v'(t) =
s″(t) represents the instantaneous acceleration of the particle at time
t.
A positive velocity indicates that the position is increasing as time increases, while a negative velocity indicates that the position is decreasing with respect to time. If the distance remains constant, then the velocity will be zero on such an interval of time. Likewise, a positive acceleration implies that the velocity is increasing with respect to time, and a negative acceleration implies that the velocity is decreasing with respect to time. If the velocity remains constant on an interval of time, then the acceleration will be zero on the interval.
Example 1: The position of a particle on a line is given by
s(t) =
t3 − 3
t2 − 6
t + 5, where
t is measured in seconds and
s is measured in feet. Find
- The velocity of the particle at the end of 2 seconds.
- The acceleration of the particle at the end of 2 seconds.
Part (a): The velocity of the particle is
Part (b): The acceleration of the particle is
Example 2: The formula
s(t) = −4.9
t2 + 49
t + 15 gives the height in meters of an object after it is thrown vertically upward from a point 15 meters above the ground at a velocity of 49 m/sec. How high above the ground will the object reach?
The velocity of the object will be zero at its highest point above the ground. That is,
v =
s′(t) = 0, where
The height above the ground at 5 seconds is
hence, the object will reach its highest point at 137.5 m above the ground.
Related Rates of Change
Some problems in calculus require finding the rate of change or two or more variables that are related to a common variable, namely time. To solve these types of problems, the appropriate rate of change is determined by implicit differentiation with respect to time. Note that a given rate of change is positive if the dependent variable increases with respect to time and negative if the dependent variable decreases with respect to time. The sign of the rate of change of the solution variable with respect to time will also indicate whether the variable is increasing or decreasing with respect to time.
Example 1: Air is being pumped into a spherical balloon such that its radius increases at a rate of .75 in/min. Find the rate of change of its volume when the radius is 5 inches.
The volume (
V) of a sphere with radius
r is
Differentiating with respect to
t, you find that
The rate of change of the radius
dr/dt = .75 in/min because the radius is increasing with respect to time.
At
r = 5 inches, you find that
hence, the volume is increasing at a rate of 75π cu in/min when the radius has a length of 5 inches.
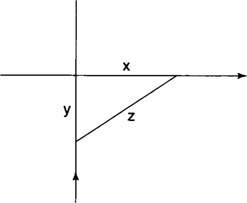
Example 2: A car is traveling north toward an intersection at a rate of 60 mph while a truck is traveling east away from the intersection at a rate of 50 mph. Find the rate of change of the distance between the car and truck when the car is 3 miles south of the intersection and the truck is 4 miles east of the intersection.
- Let x = distance traveled by the truck
- y = distance traveled by the car
- z = distance between the car and truck
The distances are related by the Pythagorean Theorem:
x2 +
y2 =
z2 (Figure
1 )
|
|
|
| Figure 1 | A diagram of the situation for Example 2. |
|
|
. The rate of change of the truck is dx/dt = 50 mph because it is traveling away from the intersection, while the rate of change of the car is dy/dt = −60 mph because it is traveling toward the intersection. Differentiating with respect to time, you find that
hence, the distance between the car and the truck is increasing at a rate of 4 mph at the time in question.
Differentials
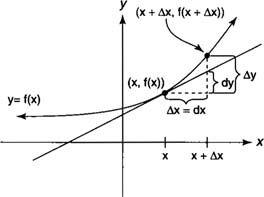
The derivative of a function can often be used to approximate certain function values with a surprising degree of accuracy. To do this, the concept of the differential of the independent variable and the dependent variable must be introduced.
The definition of the derivative of a function
y =
f(x) as you recall is
which represents the slope of the tangent line to the curve at some point (
x, f(x)). If Δ
x is very small (Δ
x ≠ 0), then the slope of the tangent is approximately the same as the slope of the secant line through (
x, f(x)). That is,
The differential of the independent variable
x is written
dx and is the same as the change in
x, Δ
x. That is,
The differential of the dependent variable
y, written
dy, is defined to be
The conclusion to be drawn from the preceding discussion is that the differential of
y(dy) is approximately equal to the exact change in
y(Δ
y), provided that the change in
x (Δ
x =
dx) is relatively small. The smaller the change in
x, the closer
dy will be to Δ
y, enabling you to approximate function values close to
f(x) (Figure
1 )
|
|
|
| Figure 1 | Approximating a function with differentials. |
|
|
. Example 1: Find dy for y = x3 + 5 x −1.
Example 2: Use differentials to approximate the change in the area of a square if the length of its side increases from 6 cm to 6.23 cm.
Let x = length of the side of the square. The area may be expressed as a function of x, where y = x2. The differential dy is
Because x is increasing from 6 to 6.23, you find that Δ x = dx = .23 cm; hence,
The area of the square will increase by approximately 2.76 cm2 as its side length increases from 6 to 6.23. Note that the exact increase in area (Δ y) is 2.8129 cm2.
Example 3: Use differentials to approximate the value of  to the nearest thousandth.
Because the function you are applying is
to the nearest thousandth.
Because the function you are applying is  , choose a convenient value of x that is a perfect cube and is relatively close to 26.55, namely x = 27. The differential dy is
, choose a convenient value of x that is a perfect cube and is relatively close to 26.55, namely x = 27. The differential dy is
Because x is decreasing from 27 to 26.55, you find that Δ x = dx = −.45; hence,
which implies that  will be approximately 1/60 less that
will be approximately 1/60 less that 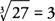 ; hence,
; hence,
to the nearest thousandth.
Note that the calculator value of 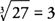 is 2.983239874, which rounds to the same answer to the nearest thousandth!
is 2.983239874, which rounds to the same answer to the nearest thousandth!
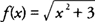 at the point (−1,2).
at the point (−1,2). 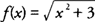 at the point (−1, 2).
at the point (−1, 2). 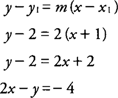
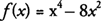 .
. 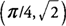 and
and 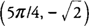
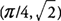 and
and 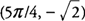 . The function values at the end points of the interval are f(0) = 1 and f(2π)=1; hence, the maximum function value of f(x) is
. The function values at the end points of the interval are f(0) = 1 and f(2π)=1; hence, the maximum function value of f(x) is 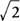 at x=π/4, and the minimum function value of f(x) is −
at x=π/4, and the minimum function value of f(x) is − 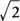 at x = 5π/4.
at x = 5π/4. 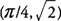 . Also f′(x) changes from negative to positive around 5π/4, and hence, f has a local minimum at
. Also f′(x) changes from negative to positive around 5π/4, and hence, f has a local minimum at 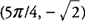
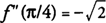 and f has a local maximum at
and f has a local maximum at 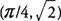 . Also,
. Also, 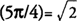 . and f has a local minimum at
. and f has a local minimum at 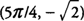 .
. to the nearest thousandth.
to the nearest thousandth.  , choose a convenient value of x that is a perfect cube and is relatively close to 26.55, namely x = 27. The differential dy is
, choose a convenient value of x that is a perfect cube and is relatively close to 26.55, namely x = 27. The differential dy is  will be approximately 1/60 less that
will be approximately 1/60 less that 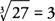 ; hence,
; hence, 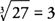 is 2.983239874, which rounds to the same answer to the nearest thousandth!
is 2.983239874, which rounds to the same answer to the nearest thousandth!