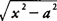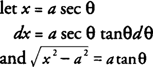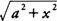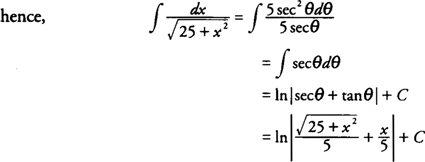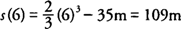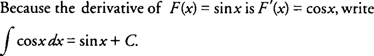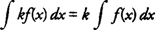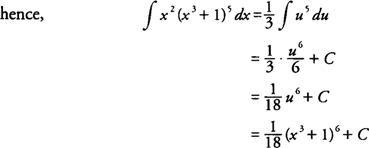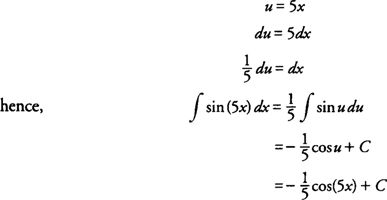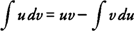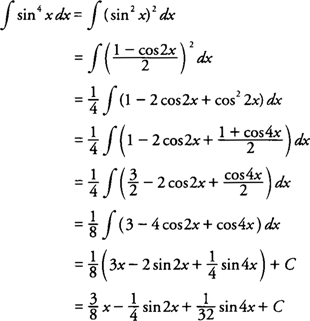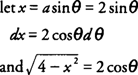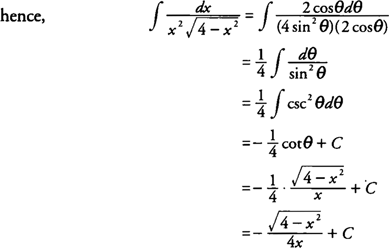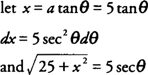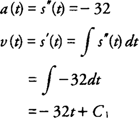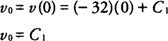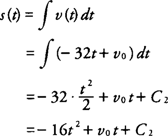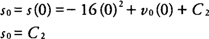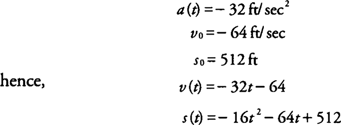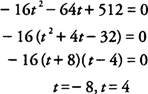Antiderivatives/Indefinite Integrals
A function
F(
x) is called an
antiderivative of a function of
f(
x) if
F′(
x) =
f(
x) for all
x in the domain of
f. Note that the function
F is not unique and that an infinite number of antiderivatives could exist for a given function. For example,
F(
x) =
x3,
G(
x) =
x3 + 5, and
H(
x) =
x3 − 2 are all antiderivatives of
f(
x) = 3
x2 because
F′(
x) =
G′(
x) =
H′(
x) =
f(
x) for all
x in the domain of
f. It is clear that these functions
F, G, and
H differ only by some constant value and that the derivative of that constant value is always zero. In other words, if
F(
x) and
G(
x) are antiderivatives of
f(
x) on some interval, then
F′(
x) =
G′(
x) and
F(
x) =
G(
x) +
C for some constant
C in the interval. Geometrically, this means that the graphs of
F(
x) and
G(
x) are identical except for their vertical position.
The notation used to represent all antiderivatives of a function
f(
x) is the
indefinite integral symbol written
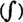
, where
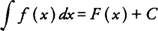
. The function of
f(
x) is called the integrand, and
C is reffered to as the constant of integration. The expression
F(
x) +
C is called the indefinite integral of
F with respect to the independent variable
x. Using the previous example of
F(
x) =
x3 and
f(
x) = 3
x2, you find that
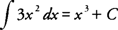
.
The indefinite integral of a function is sometimes called the general antiderivative of the function as well.
Example 1: Find the indefinite integral of
f(
x) = cos
x.
Example 2: Find the general antiderivative of
f(
x) = –8.
Because the derivative of
F(
x) = −8
x is
F′(
x) = −8, write
Integration Techniques
Many integration formulas can be derived directly from their corresponding derivative formulas, while other integration problems require more work. Some that require more work are substitution and change of variables, integration by parts, trigonometric integrals, and trigonometric substitutions.
Most of the following basic formulas directly follow the differentiation rules.
-
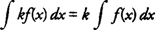
-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

Example 1: Evaluate 
Using formula (4) from the preceding list, you find that 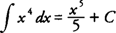 .
.
Example 2: Evaluate  .
.
Because  using formula (4) from the preceding list yields
using formula (4) from the preceding list yields
Example 3: Evaluate
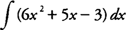
Applying formulas (1), (2), (3), and (4), you find that
Example 4: Evaluate

Using formula (13), you find that
 Example 5:
Example 5: Evaluate

Using formula (19) with a = 5, you find that
Substitution and change of variables
One of the integration techniques that is useful in evaluating indefinite integrals that do not seem to fit the basic formulas is substitution and change of variables. This technique is often compared to the chain rule for differentiation because they both apply to composite functions. In this method, the inside function of the composition is usually replaced by a single variable (often u). Note that the derivative or a constant multiple of the derivative of the inside function must be a factor of the integrand.
The purpose in using the substitution technique is to rewrite the integration problem in terms of the new variable so that one or more of the basic integration formulas can then be applied. Although this approach may seem like more work initially, it will eventually make the indefinite integral much easier to evaluate.
Note that for the final answer to make sense, it must be written in terms of the original variable of integration.
Example 6: Evaluate 
Because the inside function of the composition is x3 + 1, substitute with
Example 7: 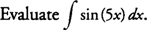
Because the inside function of the composition is 5
x, substitute with
Example 8: Evaluate

Because the inside function of the composition is 9 –
x2, substitute with
Integration by parts
Another integration technique to consider in evaluating indefinite integrals that do not fit the basic formulas is integration by parts. You may consider this method when the integrand is a single transcendental function or a product of an algebraic function and a transcendental function. The basic formula for integration by parts is
where
u and
v are differential functions of the variable of integration.
A general rule of thumb to follow is to first choose
dv as the most complicated part of the integrand that can be easily integrated to find
v. The
u function will be the remaining part of the integrand that will be differentiated to find
du. The goal of this technique is to find an integral, ∫
v du, which is easier to evaluate than the original integral.
Example 9: Evaluate ∫
x sech
2 x dx.
Example 10: Evaluate ∫
x4 In
x dx.
Example 11: Evaluate ∫ arctan
x dx.
Trigonometric integrals
Integrals involving powers of the trigonometric functions must often be manipulated to get them into a form in which the basic integration formulas can be applied. It is extremely important for you to be familiar with the basic trigonometric identities, because you often used these to rewrite the integrand in a more workable form. As in integration by parts, the goal is to find an integral that is easier to evaluate than the original integral.
Example 12: Evaluate ∫ cos3 x sin4 dx
Example 13: Evaluate ∫ sec
6 x dx
Example 14: Evaluate ∫ sin
4 x dx
Trigonometric substitutions
If an integrand contains a radical expression of the form 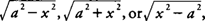 a specific trigonometric substitution may be helpful in evaluating the indefinite integral. Some general rules to follow are
a specific trigonometric substitution may be helpful in evaluating the indefinite integral. Some general rules to follow are
- If the integrand contains

- If the integrand contains

- If the integrand contains
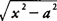
Right triangles may be used in each of the three preceding cases to determine the expression for any of the six trigonometric functions that appear in the evaluation of the indefinite integral.
Example 15: Evaluate 
Because the radical has the form 
|
|
|
| Figure 1 | Diagram for Example 15. |
|
|
Example 16: Evaluate

Because the radical has the form
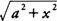
|
|
|
| Figure 2 | Diagram for Example 16. |
|
|
Distance, Velocity, and Acceleration
The indefinite integral is commonly applied in problems involving distance, velocity, and acceleration, each of which is a function of time. In the discussion of the applications of the derivative, note that the derivative of a distance function represents
instantaneous velocity and that the derivative of the velocity function represents
instantaneous acceleration at a particular time. In considering the relationship between the derivative and the indefinite integral as inverse operations, note that the indefinite integral of the acceleration function represents the velocity function and that the indefinite integral of the velocity represents the distance function.
In case of a free-falling object, the acceleration due to gravity is –32 ft/sec
2. The significance of the negative is that the rate of change of the velocity with respect to time (acceleration), is negative because the velocity is decreasing as the time increases. Using the fact that the velocity is the indefinite integral of the acceleration, you find that
Now, at
t = 0, the initial velocity (
v0) is
hence, because the constant of integration for the velocity in this situation is equal to the initial velocity, write

Because the distance is the indefinite integral of the velocity, you find that
Now, at
t = 0, the initial distance (
s0) is
hence, because the constant of integration for the distance in this situation is equal to the initial distance, write
 Example 1:
Example 1: A ball is thrown downward from a height of 512 feet with a velocity of 64 feet per second. How long will it take for the ball to reach the ground?
From the given conditions, you find that
The distance is zero when the ball reaches the ground or
hence, the ball will reach the ground 4 seconds after it is thrown.
Example 2: In the previous example, what will the velocity of the ball be when it hits the ground?
Because
v(
t) = –32(
t) – 64 and it takes 4 seconds for the ball to reach the ground, you find that
hence, the ball will hit the ground with a velocity of –192 ft/sec. The significance of the negative velocity is that the rate of change of the distance with respect to time (velocity) is negative because the distance is decreasing as the time increases.
Example 3: A missile is accelerating at a rate of 4
t m/sec
2 from a position at rest in a silo 35 m below ground level. How high above the ground will it be after 6 seconds?
From the given conditions, you find that
a(
t) = 4
t m/sec
2,
v0 = 0 m/sec because it begins at rest, and s
0 = –35 m because the missile is below ground level; hence,
After 6 seconds, you find that
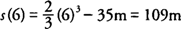
hence, the missile will be 109 m above the ground after 6 seconds.
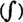 , where
, where 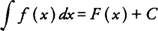 . The function of f( x) is called the integrand, and C is reffered to as the constant of integration. The expression F( x) + C is called the indefinite integral of F with respect to the independent variable x. Using the previous example of F( x) = x3 and f( x) = 3 x2, you find that
. The function of f( x) is called the integrand, and C is reffered to as the constant of integration. The expression F( x) + C is called the indefinite integral of F with respect to the independent variable x. Using the previous example of F( x) = x3 and f( x) = 3 x2, you find that 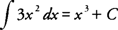 .
. 

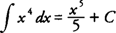 .
.  .
.  using formula (4) from the preceding list yields
using formula (4) from the preceding list yields 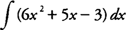




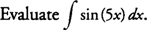

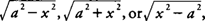 a specific trigonometric substitution may be helpful in evaluating the indefinite integral. Some general rules to follow are
a specific trigonometric substitution may be helpful in evaluating the indefinite integral. Some general rules to follow are