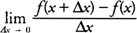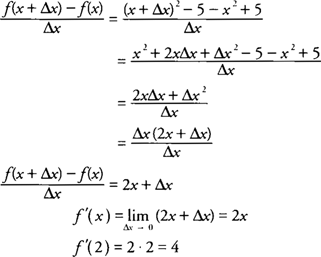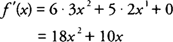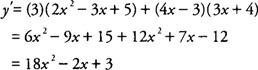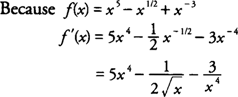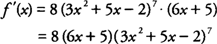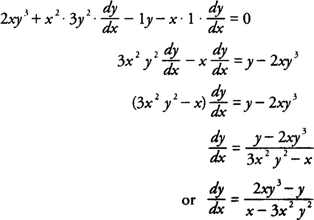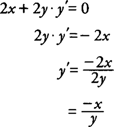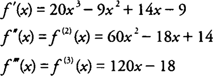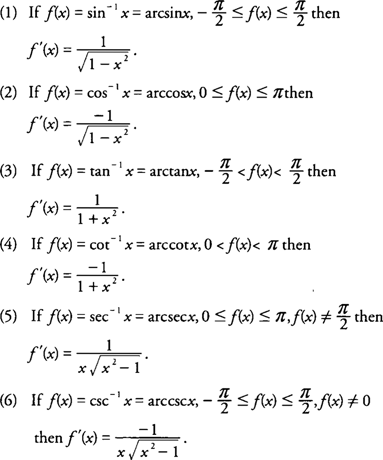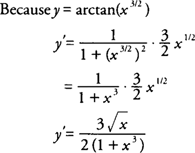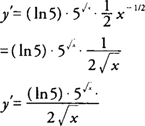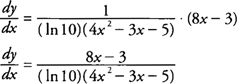Definition
One of the most important applications of limits is the concept of the
derivative of a function. In calculus, the derivative of a function is used in a wide variety of problems, and understanding it is essential to applying it to such problems.
The
derivative of a function
y =
f(
x) at a point (
x,
f(
x)) is defined as
if this limit exists. The derivative is denoted by
f′ (
x), read “
f prime of
x” or “
f prime at
x,” and
f is said to be
differentiable at
x if this limit exists (see Figure
1 ).
|
| |
|
| Figure 1 | The derivative of a function as the limit of rise over run.
|
|
|
If a function is differentiable at
x, then it must be continuous at
x, but the converse is not necessarily true. That is, a function may be continuous at a point, but the derivative at that point may not exist. As an example, the function
f(
x) =
x1/3 is continuous over its entire domain or real numbers, but its derivative does not exist at
x = 0.
Another example is the function
f(
x) = |
x + 2|, which is also continuous over its entire domain of real numbers but is not differentiable at
x = −2.
The relationship between continuity and differentiability can be summarized as follows: Differentiability implies continuity, but continuity
does not imply differentiability.
Example 1: Find the derivative of
f(
x) =
x2 − 5 at the point (2,−1).
hence, the derivative of
f(
x) =
x2 − 5 at the point (2,−1) is 4. One interpretation of the derivative of a function at a point is the
slope of the tangent line at this point. The derivative may be thought of as the limit of the slopes of the secant lines passing through a fixed point on a curve and other points on the curve that get closer and closer to the fixed point. If this limit exists, it is defined to be the slope of the tangent line at the fixed point, (
x,
f(
x)) on the graph of
y =
f(
x).
Another interpretation of the derivative is the
instantaneous velocity of a function representing the position of a particle along a line at time
t, where
y =
s(
t). The derivative may be thought of as a limit of the average velocities between a fixed time and other times that get closer and closer to the fixed time. If this limit exists, it is defined to be the instantaneous velocity at time
t for the function,
y =
s(
t).
A third interpretation of the derivative is the
instantaneous rate of change of a function at a point. The derivative may be thought of as the limit of the average rates of change between a fixed point and other points on the curve that get closer and closer to the fixed point. If this limit exists, it is defined to be the instantaneous rate of change at the fixed point (
x,
f(
x)) on the graph of
y =
f(
x).
Example 2: Find the instantaneous velocity of
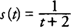
at the time
t = 3.
hence, the instantaneous velocity of
s(
t) = 1/(
t + 2) at time
t = 3 is −1/25. The negative velocity indicates that the particle is moving in the negative direction. A number of different notations are used to represent the derivative of a function
y =
f(
x) with
f′ (
x) being most common. Some others are
y′,
dy/dx,
df/
dx,
df(
x)/
dx,
D x f, and
D x f(
x), and you should be able to use any of these in selected problems.
Differentation Rules
Many differentiation rules can be proven using the limit definition of the derivative and are also useful in finding the derivatives of applicable functions. To eliminate the need of using the formal definition for every application of the derivative, some of the more useful formulas are listed here.
- If f( x) = c, where c is a constant, the f′ ( x) = 0.
- If f( x) = c · g( x), then f′ ( x) = c · g′ ( x).
- Sum Rule: If f( x) = g( x) + h( x), then f′ ( x) = g′ ( x) + h′ ( x).
- Difference Rule: If f( x) = g( x) − h( x), then f′ ( x) = g′ ( x) − h′ ( x).
- Product Rule: If f( x) = g( x) · h( x), then f′ ( x)= g′ ( x) · h( x)+ h′ ( x) · g( x).
Example 1: Find
f′ (
x) if
f (
x) = 6
x3 + 5
x2 + 9.
Example 2: Find
y′ if
y = (3
x + 4)(2
x2 − 3
x + 5).
Example 3: Find

if
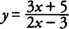
.
Example 4: Find
f′(
x) if
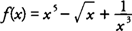
.
Example 5: Find
f′(3) if
f (
x) =
x2 − 8
x +3.
Example 6: If
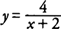
, find
y′ at (2,1).
Example 7: Find the slope of the tangent line to the curve
y = 12 − 3
x2 at the point (−1,9).
Because the slope of the tangent line to a curve is the derivative, you find that
y′ = −6
x; hence, at (−1,9),
y′ = 6, and the tangent line has slope 6 at the point (−1,9).
Trigonometric Function Differentiation
The six trigonometric functions also have differentiation formulas that can be used in application problems of the derivative. The rules are summarized as follows:
- If f( x) = sin x, then f′( x) = cos x
- If f( x) = cos x, then f′( x) = −sin x
- If f( x) = tan x, then f′( x) = sec2 x
- If f( x) = cot x, then f′( x) = −csc2 x.
- If f( x) = sec x, then f′( x) = sec x tan x
- If f( x) = csc x, then f′( x) = −csc x cot x
Example 3: Find
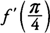
if
f(
x) = 5 sin
x + cos
x.
Example 4: Find the slope of the tangent line to the curve
y = sin
x at the point (π/2,1)
Because the slope of the tangent line to a curve is the derivative, you find that
y′ = cos
x; hence, at (π/2,1),
y′ = cos π/2 = 0, and the tangent line has a slope 0 at the point (π/2,1). Note that the geometric interpretation of this result is that the tangent line is horizontal at this point on the graph of
y = sin
x.
Chain Rule
The
chain rule provides us a technique for finding the derivative of composite functions, with the number of functions that make up the composition determining how many differentiation steps are necessary. For example, if a composite function
f(
x) is defined as
Note that because two functions,
g and
h, make up the composite function
f, you have to consider the derivatives
g′ and
h′ in differentiating
f(
x).
If a composite function
r(
x) is defined as
Here, three functions—
m,
n, and
p—make up the composition function
r; hence, you have to consider the derivatives
m′,
n′, and
p′ in differentiating
r(
x). A technique that is sometimes suggested for differentiating composite functions is to work from the “outside to the inside” functions to establish a sequence for each of the derivatives that must be taken.
Example 1: Find
f′(
x) if
f(
x) = (3x
2 + 5x − 2)
8.
Example 2: Find
f′(
x) if
f(
x) = tan (sec
x).
Example 3: Find
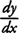
if
y = sin
3 (3
x − 1).
Example 4: Find
f′(2) if
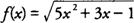
.
Example 5: Find the slope of the tangent line to a curve
y = (
x2 − 3)
5 at the point (−1, −32).
Because the slope of the tangent line to a curve is the derivative, you find that
which represents the slope of the tangent line at the point (−1,−32).
Implicit Differentiation
In mathematics, some equations in
x and
y do not explicitly define
y as a function
x and cannot be easily manipulated to solve for
y in terms of
x, even though such a function may exist. When this occurs, it is implied that there exists a function
y =
f(
x) such that the given equation is satisfied. The technique of
implicit differentiation allows you to find the derivative of
y with respect to
x without having to solve the given equation for
y. The chain rule must be used whenever the function
y is being differentiated because of our assumption that
y may be expressed as a function of
x.
Example 1: Find
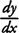
if
x2 y3 −
xy = 10.
Differentiating implicitly with respect to
x, you find that
Example 2: Find
y′ if
y = sin
x + cos
y.
Differentiating implicitly with respect to
x, you find that
Example 3: Find
y′ at (−1,1) if
x2 + 3
xy +
y2 = −1.
Differentiating implicitly with respect to
x, you find that
Example 4: Find the slope of the tangent line to the curve
x2 +
y2 = 25 at the point (3,−4).
Because the slope of the tangent line to a curve is the derivative, differentiate implicitly with respect to
x, which yields
hence, at (3,−4),
y′ = −3/−4 = 3/4, and the tangent line has slope 3/4 at the point (3,−4).
Higher Order Derivatives
Because the derivative of a function
y =
f(
x) is itself a function
y′ =
f′(
x), you can take the derivative of
f′(
x), which is generally referred to as the
second derivative of f(x) and written
f“(
x) or
f2(
x). This differentiation process can be continued to find the third, fourth, and successive derivatives of
f(
x), which are called
higher order derivatives of
f(
x). Because the “prime” notation for derivatives would eventually become somewhat messy, it is preferable to use the numerical notation
f(
n )(
x) =
y(
n ) to denote the
nth derivative of
f(
x).
Example 1: Find the first, second, and third derivatives of
f(
x) = 5
x4 − 3x
3 + 7x
2 − 9x + 2.
Example 2: Find the first, second, and third derivatives of
y = sin
2 x.
Example 3: Find
f(3) (4) if

.
Differentiation of Inverse Trigonometric Functions
Each of the six basic trigonometric functions have corresponding inverse functions when appropriate restrictions are placed on the domain of the original functions. All the inverse trigonometric functions have derivatives, which are summarized as follows:
Example 1: Find
f′(
x) if
f(
x) = cos
−1(5
x).
Example 2: Find
y′ if

.
Differentiation of Exponential and Logarithmic Functions
Exponential functions and their corresponding inverse functions, called
logarithmic functions, have the following differentiation formulas:
Note that the exponential function
f(
x) =
ex has the special property that its derivative is the function itself,
f′(
x) =
ex =
f(
x).
Example 1: Find
f′(
x) if
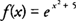 Example 2:
Example 2: Find
y′ if

.
Example 3: Find
f′(
x) if
f(
x) = 1n(sin
x).
Example 4: Find

if
y=log
10(4
x2 − 3
x −5).
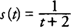 at the time t = 3.
at the time t = 3. 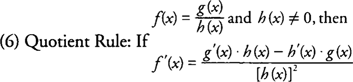
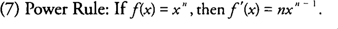
 if
if 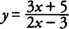 .
. 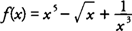 .
. 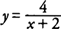 , find y′ at (2,1).
, find y′ at (2,1). 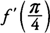 if f( x) = 5 sin x + cos x.
if f( x) = 5 sin x + cos x. 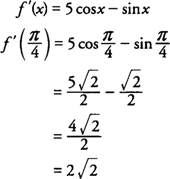
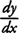 if y = sin3 (3 x − 1).
if y = sin3 (3 x − 1). 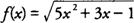 .
. 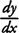 if x2 y3 − xy = 10.
if x2 y3 − xy = 10.  .
. 
 .
. 
 .
.  if y=log10(4 x2 − 3 x −5).
if y=log10(4 x2 − 3 x −5).