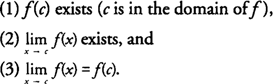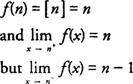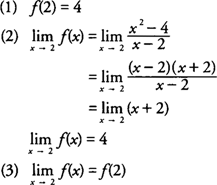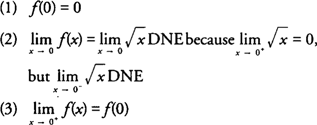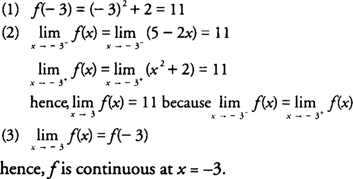Published On:Friday, 9 December 2011
Posted by Muhammad Atif Saeed
Continuity
Continuity
A function f( x) is said to be continuous at a point ( c, f( c)) if each of the following conditions is satisfied:
|
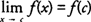and continuous at ( c, f( c)) from the left if 
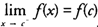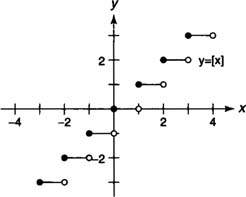
. Many of our familiar functions such as linear, quadratic and other polynomial functions, rational functions, and the trigonometric functions are continuous at each point in their domain. A special function that is often used to illustrate one-sided limits is the greatest integer function. The greatest integer function, [ x], is defined to be the largest integer less than or equal to x (see Figure 1 ).
| | |||
| |||
| | |||
| |||
| |
|
The greatest integer function is continuous at any integer n from the right only because
|
hence,
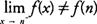and f( x) is not continuous at n from the left. Note that the greatest integer function is continuous from the right and from the left at any noninteger value of x. Example 1: Discuss the continuity of f( x) = 2 x + 3 at x = −4.
When the definition of continuity is applied to f( x) at x = −4, you find that
|
hence, f is continous at x = −4.
Example 2: Discuss the continuity of
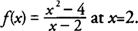
When the definition of continuity is applied to f( x) at x = 2, you find that f(2) does not exist; hence, f is not continuous (discontinuous) at x = 2.
Example 3: Discuss the continuity of
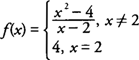
When the definition of continuity is applied to f( x) at x = 2, you find that
|
hence, f is continous at x = 2.
Example 4: Discuss the continuity of
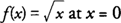. When the definition of continuity is applied to f( x) at x = 0, you find that
|
hence, f is continuous at x = 0 from the right only.
Example 5: Discuss the continuity of
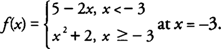
When the definition of continuity is applied to f( x) at x = −3, you find that
|
Many theorems in calculus require that functions be continuous on intervals of real numbers. A function f( x) is said to be continuous on an open interval ( a, b) if f is continuous at each point c ∈ ( a, b). A function f( x) is said to be continuous on a closed interval [ a, b] if f is continuous at each point c ∈ ( a, b) and if f is continuous at a from the right and continuous at b from the left.
Example 6:
- f( x) = 2 x + 3 is continuous on (−∞,+∞) because f is continuous at every point c ∈ (−∞,+∞).
- f( x) = ( x − 3)/( x + 4) is continuous on (−∞,−4) and (−4,+∞) because f is continuous at every point c ∈ (−∞,−4) and c ∈ (−4,+∞)
- f( x) = ( x − 3)/( x + 4) is not continuous on (−∞,−4] or [−4,+∞) because f is not continuous on −4 from the left or from the right.
-
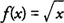is continuous on [0, +∞) because f is continuous at every point c ∈ (0,+∞) and is continuous at 0 from the right.
- f( x) = cos x is continuous on (−∞,+∞) because f is continuous at every point c ∈ (−∞,+∞).
- f( x) = tan x is continuous on (0,π/2) because f is continuous at every point c ∈ (0,π/2).
- f( x) = tan x is not continuous on [0,π/2] because f is not continuous at π/2 from the left.
- f( x) = tan x is continuous on [0,π/2) because f is continuous at every point c ∈ (0,π/2) and is continuous at 0 from the right.
- f( x) = 2 x/( x2 + 5) is continuous on (−∞,+∞) because f is continuous at every point c ∈ (−∞,+∞).
- f( x) = | x − 2|/( x − 2) is continuous on (−∞,2) and (2,+∞) because f is continuous at every point c ∈ (−∞,2) and c ∈ (2,+∞).
- f( x) = | x − 2|/( x − 2) is not continuous on (−∞,2] or [2,+∞) because f is not continuous at 2 from the left or from the right.
