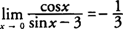Limits Involving Trigonometric Functions

The trigonometric functions sine and cosine have four important limit properties:

You can use these properties to evaluate many limit problems involving the six basic trigonometric functions.
Example 1: Evaluate .
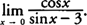Substituting 0 for x, you find that cos x approaches 1 and sin x − 3 approaches −3; hence,


Example 2: Evaluate
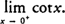
Because cot x = cos x/sin x, you find 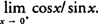The numerator approaches 1 and the denominator approaches 0 through positive values because we are approaching 0 in the first quadrant; hence, the function increases without bound and 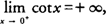and the function has a vertical asymptote at x = 0.
Example 3: Evaluate
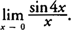
Multiplying the numerator and the denominator by 4 produces


Example 4: Evaluate .
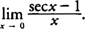Because sec x = 1/cos x, you find that

About the Author

By Muhammad Atif Saeed on 01:56. Filed under Calculus , feature , Mathandstat . Follow any responses to the RSS 2.0. Leave a response