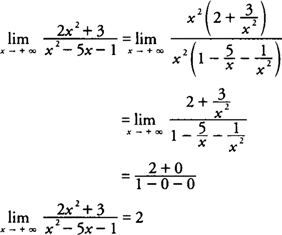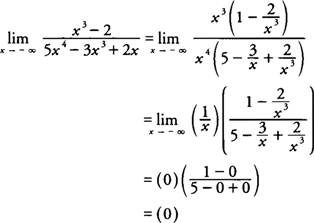Published On:Friday, 9 December 2011
Posted by Muhammad Atif Saeed
Limits at Infinity
Limits at Infinity
Limits at infinity are used to describe the behavior of functions as the independent variable increases or decreases without bound. If a function approaches a numerical value L in either of these situations, write| |
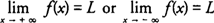 |
Evaluate 1: Evaluate
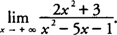
Factor the largest power of x in the numerator from each term and the largest power of x in the denominator from each term.
You find that
|
The function has a horizontal asymptote at y = 2.
Example 2: Evaluate
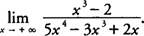
Factor x3 from each term in the numerator and x4 from each term in the denominator, which yields
|
The function has a horizontal asymptote at y = 0.
Example 3: Evaluate
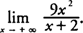 .
. Factor x2 from each term in the numerator and x from each term in the denominator, which yields
|
Because this limit does not approach a real number value, the function has no horizontal asymptote as x increases without bound.
Example 4: Evaluate
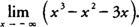 .
. Factor x3 from each term of the expression, which yields
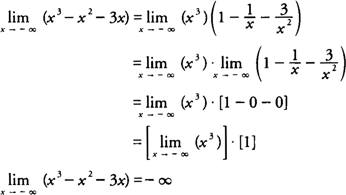 |
| |
As in the previous example, this function has no horizontal asymptote as x decreases without bound.