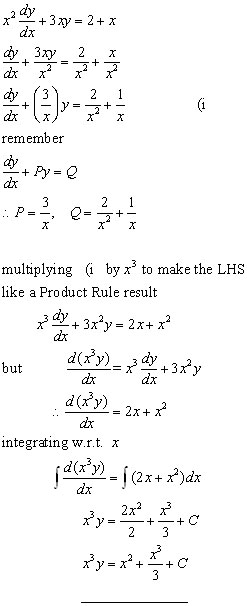Published On:Friday, 16 December 2011
Posted by Muhammad Atif Saeed
Integration: Differential Equations
Introduction
All equations with derivatives of a variable w.r.t. another are called 'differential equations'. A first order differential equation contains a first derivative eg dy/dx.
It might not be appreciated, but ALL integrals are derived from original 'first-order' differential equations.
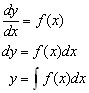
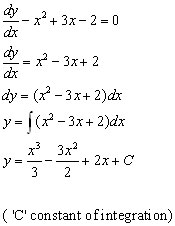
First Order with 'variables separable'
Solution is by collecting all the 'y' terms on one side, all the 'x' terms on the other and integrating each expression independently.
Example #1
Example #2
First Order 'linear' differential equations
By definition 'linear' differential equation have the form:
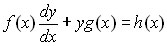
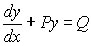
 Example
Example
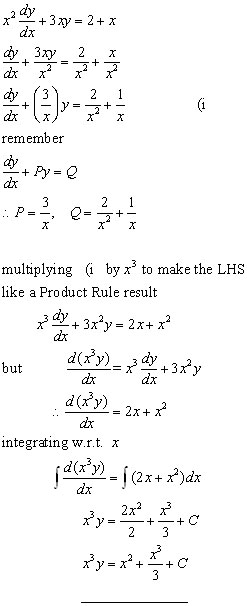
All equations with derivatives of a variable w.r.t. another are called 'differential equations'. A first order differential equation contains a first derivative eg dy/dx.
It might not be appreciated, but ALL integrals are derived from original 'first-order' differential equations.
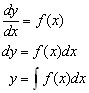
Example:
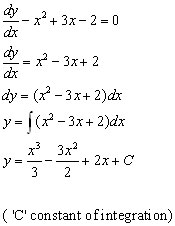
First Order with 'variables separable'
Solution is by collecting all the 'y' terms on one side, all the 'x' terms on the other and integrating each expression independently.
Example #1
Note how the constant of integration C changes its value.
Example #2
First Order 'linear' differential equations
By definition 'linear' differential equation have the form:
Dividing by f(x) to make the coefficient of dy/dx equal to '1', the equation becomes:
(where P and Q are functions of x, and only x)
The key to solving these types of problem is to choose a multiplying factor(sometimes called an 'integrating factor') to make the LHS of the equation appear like a result from the Product Rule.