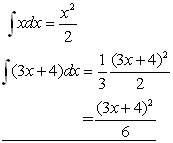Published On:Friday, 16 December 2011
Posted by Muhammad Atif Saeed
The Integration Formula
The expression to be integrated is the derivative of some function eg f(x) called the integrand.
When this expression is integrated the original function is restored plus a constant (C) called the constant of integration.
This is called the indefinite integral when the integration is not between two limiting values of x.
However when the integration is between two limiting values of x then the integral is called the definite integral and the constant of integration is not involved.
For any variable 'x' to the power of 'n' the integral is given by:
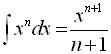
In other words, increase the power of x by '1' and divide x by the new index.
Rule #1
Any constant(eg C) multiplied by a function f(x) can be integrated by placing the constant before the integration sign.
Rule #2
The integral of two separate functions which are added together is the same as each function integrated separately then added together.
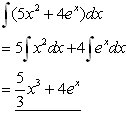
Rule #3
The addition of a constant to a variable doesn't change the form of the integral. However, x must be in the first degree ie no higher powers of x are involved. ('a' is a constant)
Rule #4
If 'a' & 'b' are constants then x can be replaced by 'bx+a' with the integral remaining in the same form.