Published On:Wednesday, 14 December 2011
Posted by Muhammad Atif Saeed
Probability
Introduction to Probability
Probability theory plays a central role in statistics. After all, statistical analysis is applied to a collection of data in order to discover something about the underlying events. These events may be connected to one another—for example, mutually exclusive—but the individual choices involved are assumed to be random. Alternatively, we may sample a population at random and make inferences about the population as a whole from the sample by using statistical analysis. Therefore, a solid understanding of probability theory—the study of random events—is necessary to understand how statistical analysis works and also to correctly interpret the results.You have an intuition about probability. As you will see, in some cases, probability theory seems obvious. But be careful: Occasionally, a seemingly obvious answer will turn out to be wrong—because sometimes your intuition about probability will fail. Even in seemingly simple cases, it is best to follow the rules of probability rather than rely on your hunche
Classic Theory
The classic theory of probability underlies much of probability in statistics. Briefly, this theory states that the chance of a particular outcome occurring is determined by the ratio of the number of favorable outcomes (or “successes”) to the total number of outcomes. Expressed as a formula,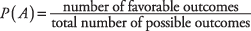
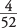 . Four is the number of favorable outcomes (the number of aces in the deck), and 52 is the number of total outcomes (the number of cards in the deck). The probability of randomly selecting an ace in one draw from a deck of cards is, therefore,
. Four is the number of favorable outcomes (the number of aces in the deck), and 52 is the number of total outcomes (the number of cards in the deck). The probability of randomly selecting an ace in one draw from a deck of cards is, therefore, 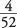 , or 0.077. In statistical analysis, probability is usually expressed as a decimal and ranges from a low of 0 (no chance) to a high of 1 (certainty).
, or 0.077. In statistical analysis, probability is usually expressed as a decimal and ranges from a low of 0 (no chance) to a high of 1 (certainty). The classic theory assumes that all outcomes have equal likelihood of occurring. In the example just cited, each card must have an equal chance of being chosen—no card is larger than any other or in any way more likely to be chosen than any other card.
The classic theory pertains only to outcomes that are mutually exclusive (or disjoint), which means that those outcomes may not occur at the same time. For example, one coin flip can result in a head or a tail, but one coin flip cannot result in a head and a tail. So, the outcome of a head and the outcome of a tail are said to be “mutually exclusive” in one coin flip, as is the outcome of an ace and a king in one card being drawn.
Relative Frequency Theory
The relative frequency theory of probability holds that if an experiment is repeated an extremely large number of times and a particular outcome occurs a percentage of the time, then that particular percentage is close to the probability of that outcome.For example, if a machine produces 10,000 widgets one at a time, and 1,000 of those widgets are faulty, the probability of that machine producing a faulty widget is approximately 1,000 out of 10,000, or 0.10.
Probability of Simple Events
Example 1
What is the probability of simultaneously flipping three coins—a penny, a nickel, and a dime—and having all three land heads?Using the classic theory, determine the ratio of the number of favorable outcomes to the number of total outcomes. Table 1 lists all possible outcomes.
There are eight different outcomes, only one of which is favorable (Outcome 1, all three coins landing heads); therefore, the probability of three coins landing heads is
 , or 0.125.
, or 0.125. What is the probability of exactly two of the three coins landing heads? Again, there are the eight total outcomes, but in this case only three favorable outcomes (outcomes 2, 3, and 5); thus, the probability of exactly two of three coins landing heads is
 , or 0.375.
, or 0.375.| Outcome | Penny | Nickel | Dime |
|---|---|---|---|
| 1 | Head | Head | Head |
| 2 | Head | Head | Tail |
| 3 | Head | Tail | Head |
| 4 | Head | Tail | Tail |
| 5 | Tail | Head | Head |
| 6 | Tail | Head | Tail |
| 7 | Tail | Tail | Head |
| 8 | Tail | | Tail |
Independent Events
Each of the three coins being flipped in the preceding example is what is known as an independent event. Independent events are defined as outcomes that are not affected by other outcomes. In other words, the flip of the penny does not affect the flip of the nickel, and vice versa.Dependent Events
Dependent events, on the other hand, are outcomes that are affected by other outcomes. Consider the following example.Example 1
What is the probability of randomly drawing an ace from a deck of cards and then drawing an ace again from the same deck of cards, without returning the first drawn card back to the deck?For the first draw, the probability of a favorable outcome is
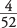 , as explained earlier; however, after that first card has been drawn, the total number of outcomes is no longer 52, but now 51 because a card has been removed from the deck. And if that first card drawn resulted in a favorable outcome (an ace), there would now be only three aces in the deck. If that first card drawn were not an ace, the number of favorable outcomes would remain at four. So, the second draw is a dependent event because its probability changes depending upon what happens on the first draw.
, as explained earlier; however, after that first card has been drawn, the total number of outcomes is no longer 52, but now 51 because a card has been removed from the deck. And if that first card drawn resulted in a favorable outcome (an ace), there would now be only three aces in the deck. If that first card drawn were not an ace, the number of favorable outcomes would remain at four. So, the second draw is a dependent event because its probability changes depending upon what happens on the first draw. If, however, you replace that drawn card back into the deck and shuffle well again before the second draw, then the probability for a favorable outcome for each draw will now be equal
 , and these events will be independent.
, and these events will be independent.Probability of Joint Occurrences
Another way to compute the probability of all three flipped coins landing heads is as a series of three different events: First flip the penny, then flip the nickel, and then flip the dime. Will the probability of landing three heads still be 0.125?Multiplication rule
To compute the probability of joint occurrence (two or more independent events all occurring), multiply their probabilities.For example, the probability of the penny landing heads is
 , or 0.5; the probability of the nickel next landing heads is
, or 0.5; the probability of the nickel next landing heads is  , or 0.5; and the probability of the dime landing heads is
, or 0.5; and the probability of the dime landing heads is  , or 0.5. Thus, note that
, or 0.5. Thus, note that 0.5 × 0.5 × 0.5 = 0.125
which is what you determined with the classic theory by assessing the ratio of the number of favorable outcomes to the number of total outcomes. The notation for joint occurrence is P( A∩ B) = P( A) × P( B)
which is read: The probability of A and B both happening is equal to the probability of A times the probability of B.Using the multiplication rule, you also can determine the probability of drawing two aces in a row from a deck of cards. The only way to draw two aces in a row from a deck of cards is for both draws to be favorable. For the first draw, the probability of a favorable outcome is
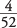 . But because the first draw is favorable, only three aces are left among 51 cards. So, the probability of a favorable outcome on the second draw is
. But because the first draw is favorable, only three aces are left among 51 cards. So, the probability of a favorable outcome on the second draw is 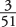 . For both events to happen, you simply multiply those two probabilities together:
. For both events to happen, you simply multiply those two probabilities together: 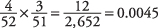
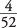 , because these events are now independent. Drawing an ace twice in a row, with the odds being
, because these events are now independent. Drawing an ace twice in a row, with the odds being 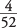 both times, gives the following:
both times, gives the following: 
Addition rule
Given mutually exclusive events, finding the probability of at least one of them occurring is accomplished by adding their probabilities.For example, what is the probability of one coin flip resulting in at least one head or at least one tail?
The probability of one coin flip landing heads is 0.5, and the probability of one coin flip landing tails is 0.5. Are these two outcomes mutually exclusive in one coin flip? Yes, they are. You cannot have a coin land both heads and tails in one coin flip; therefore, you can determine the probability of at least one head or one tail resulting from one flip by adding the two probabilities:
0.5 + 0.5 = 1 (or certainty)
Example 1
What is the probability of at least one spade or one club being randomly chosen in one draw from a deck of cards?The probability of drawing a spade in one draw is
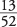 ; the probability of drawing a club in one draw is
; the probability of drawing a club in one draw is 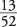 . These two outcomes are mutually exclusive in one draw because you cannot draw both a spade and a club in one draw; therefore, you can use the addition rule to determine the probability of drawing at least one spade or one club in one draw:
. These two outcomes are mutually exclusive in one draw because you cannot draw both a spade and a club in one draw; therefore, you can use the addition rule to determine the probability of drawing at least one spade or one club in one draw: 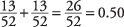
Non-Mutually-Exclusive Outcomes
For the addition rule to apply, the events must be mutually exclusive. Now consider the following example.Example 1
What is the probability of the outcome of at least one head in two coin flips?Should you add the two probabilities as in the preceding examples? In the first example, you added the probability of getting a head and the probability of getting a tail because those two events were mutually exclusive in one flip. In the second example, the probability of getting a spade was added to the probability of getting a club because those two outcomes were mutually exclusive in one draw. Now when you have two flips, should you add the probability of getting a head on the first flip to the probability of getting a head on the second flip? Are these two events mutually exclusive?
Of course, they are not mutually exclusive. You can get an outcome of a head on one flip and a head on the second flip. So, because they are not mutually exclusive, you cannot use the addition rule. If you did use the addition rule, you would get

Double-Counting
By using the addition rule in a situation that is not mutually exclusive, you are double-counting. One way of realizing that you are double-counting is to use the classic theory of probability: List all the different outcomes when flipping a coin twice and assess the ratio of favorable outcomes to total outcomes (see Table 1).| First Flip | with | Second Flip |
|---|---|---|
| Head | + | Head |
| Head | + | Tail |
| Tail | + | Head |
| Tail | + | Tail |
 , or 0.75, not 1. But if you had used the addition rule, you would have added the two heads from the first flip to the two heads from the second flip and gotten four heads in four flips,
, or 0.75, not 1. But if you had used the addition rule, you would have added the two heads from the first flip to the two heads from the second flip and gotten four heads in four flips, 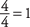 . But the two heads in that first pair constitute only one outcome; so, by counting both heads for that outcome, you are double-counting because this is the joint-occurrence outcome that is not mutually exclusive.
. But the two heads in that first pair constitute only one outcome; so, by counting both heads for that outcome, you are double-counting because this is the joint-occurrence outcome that is not mutually exclusive. To use the addition rule in a non-mutually-exclusive situation, you must subtract any events that double-count. In this case:
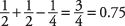
P( A∪ B) = P( A) + P( B) – P( A∩ B)
which is read: The probability of at least one of the events A or B equals the probability of A plus the probability of B minus the probability of their joint occurrence. (Note that if they are mutually exclusive, then P( A∩ B)—the joint occurrence—equals 0, and you simply add the two probabilities.) Example 1
What is the probability of drawing either a spade or an ace from a deck of cards?The probability of drawing a spade is
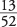 ; the probability of drawing an ace is
; the probability of drawing an ace is 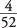 . But the probability of their joint occurrence (an ace of spades) is
. But the probability of their joint occurrence (an ace of spades) is 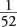 . Thus,
. Thus, 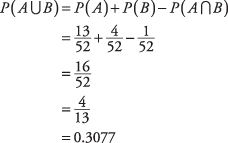
Conditional Probability
Sometimes you have more information than simply total outcomes and favorable outcomes; hence, you are able to make more informed judgments regarding probabilities. For example, suppose you know the following information: In a particular village, there are 60 women and 40 men. Twenty of those women are 70 years of age or older; five of the men are 70 years of age or older (see Table 1).| 70 or older | 69 or younger | Totals | |
|---|---|---|---|
| Women | 20 | 40 | 60 |
| Men | 5 | 35 | 40 |
| Total | 25 | 75 | 100 |
What is the probability that a person 70 years of age or older, selected at random, will be a woman? This question is different because the probability of A (being a woman) given B (the person in question being 70 years of age or older) is now conditional upon B (being 70 years of age or older). Because women number 20 out of the 25 people in the 70-or-older group, the probability of this latter question is
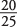 , or 0.80.
, or 0.80. Conditional probability is found using this formula:
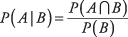
Probability Distributions
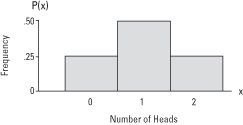
A probability distribution is a pictorial display of the probability— P( x) —for any value of x. Consider the number of possible outcomes of two coins being flipped (see Table 1). Table 2 shows the probability distribution of the results of flipping two coins. Figure 1 displays this information graphically.| Head + head | = | 2 heads |
| Head + tail | = | 1 head |
| Tail + head | = | 1 head |
| Tail + tail | = | 0 heads |
| x | P(x) |
|---|---|
| 0 |  , or 0.25 , or 0.25 |
| 1 | 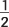 , or 0.50 , or 0.50 |
| 2 |  , or 0.25 , or 0.25 |
Figure 1. Probability distribution of the results of flipping two coins.
Discrete versus continuous variables
The number of heads resulting from coin flips can be counted only in integers (whole numbers). The number of aces drawn from a deck can be counted only in integers. These “countable” numbers are known as discrete variables: 0, 1, 2, 3, 4, and so forth. Nothing in between two variables is possible. For example, 2.6 is not possible.Qualities such as height, weight, temperature, distance, and so forth, however, can be measured using fractions or decimals as well: 34.27, 102.26, and so forth. These are known as continuous variables.
Total of probabilities of discrete variables
The probability of a discrete variable lies somewhere between 0 and 1, inclusive. For example, the probability of tossing one head in two coin flips is, as earlier, 0.50. The probability of tossing two heads in two coin flips is 0.25, and the probability of tossing no heads in two coin flips is 0.25. The sum (total) of probabilities for all values of x always equals 1. For example, note that in Tables 1 and 2, adding the probabilities for all the possible outcomes yields a sum of 1.The Binomial
A discrete variable that can result in only one of two outcomes is called binomial. For example, a coin flip is a binomial variable, but drawing a card from a standard deck of 52 is not. Whether a drug is successful or unsuccessful in producing results is a binomial variable, as is whether a machine produces perfect or imperfect widgets.Binomial experiments
Binomial experiments require the following elements:- The experiment consists of a number of identical events ( n).
- Each event has only one of two mutually exclusive outcomes. (These outcomes are called successes and failures.)
- The probability of a success outcome is equal to some percentage, which is identified as a proportion, π.
- This proportion, π, remains constant throughout all events and is defined as the ratio of number of successes to number of trials.
- The events are independent.
- Given all the above, the binomial formula can be applied ( x = number of favorable outcomes; n = number of events):
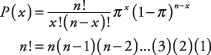
Example 1
A coin is flipped ten times. What is the probability of getting exactly five heads? Using the binomial formula, where n (the number of events) is given as 10; x (the number of favorable outcomes) is given as 5; and the probability of landing a head in one flip is 0.5: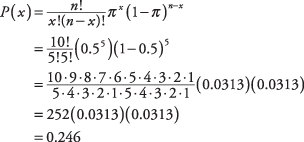
Binomial table
Because probabilities of binomial variables are so common in statistics, tables are used to alleviate having to continually use the formula. Refer to Table 1 in "Statistics Tables," and you will find that given n = 10, x = 5, and π = 0.5, the probability is 0.2461.Mean and standard deviation
The mean of the binomial probability distribution is determined by the following formula:μ = nπ
where π is the proportion of favorable outcomes and n is the number of events. The standard deviation of the binomial probability distribution is determined by this formula:

Example 2
What is the mean and standard deviation for a binomial probability distribution for ten coin flips of a fair coin?Because the proportion of favorable outcomes of a fair coin falling heads (or tails) is π = 0.5, simply substitute into the formulas:
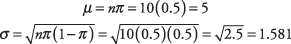
Note that this distribution appears to display symmetry. Only a binomial distribution with π = 0.5 will be truly symmetric. All other binomial distribution will be skewed.
Figure 1. The binomial probability distribution of the number of heads resulting from ten coin tosses.










