Published On:Thursday, 8 December 2011
Posted by Muhammad Atif Saeed
Solving Systems of Equations (Simultaneous Equations)
Solving Systems of Equations (Simultaneous Equations)
If you have two different equations with the same two unknowns in each, you can solve for both unknowns. There are three common methods for solving: addition/subtraction, substitution, and graphing.Addition/subtraction method
This method is also known as the elimination method.To use the addition/subtraction method, do the following:
- Multiply one or both equations by some number(s) to make the number in front of one of the letters (unknowns) the same or exactly the opposite in each equation.
- Add or subtract the two equations to eliminate one letter.
- Solve for the remaining unknown.
- Solve for the other unknown by inserting the value of the unknown found in one of the original equations.
Example 1
Solve for x and y.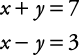
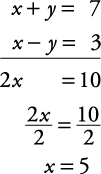
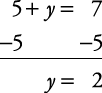
By replacing each x with a 5 and each y with a 2 in the original equations, you can see that each equation will be made true.
Example 2
Solve for x and y.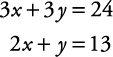
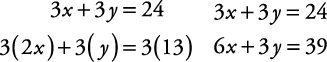
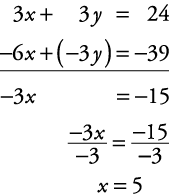
Of course, if the number in front of a letter is already the same in each equation, you do not have to change either equation. Simply add or subtract.
To check the solution, replace each x in each equation with 5 and replace each y in each equation with 3.
Example 3
Solve for a and b.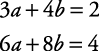
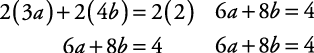
This statement is always true.
When this occurs, the system of equations does not have a unique solution. In fact, any a and b replacement that makes one of the equations true, also makes the other equation true. For example, if a = –6 and b = 5, then both equations are made true.
[3(– 6) + 4(5) = 2 AND 6(– 6) + 8(5) = 4]
What we have here is really only one equation written in two different ways. In this case, the second equation is actually the first equation multiplied by 2. The solution for this situation is either of the original equations or a simplified form of either equation.Example 4
Solve for x and y.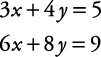
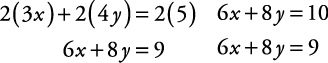
Example 5
Solve for x and y.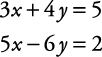
- Select a letter to eliminate.
- Use the two numbers to the left of this letter. Find the least common multiple of this value as the desired number to be in front of each letter.
- Determine what value each equation needs to be multiplied by to obtain this value and multiply the equation by that number.
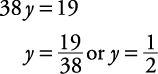
and solve for x (method 1 that follows), or start with the original two equations and eliminate y in order to solve for x (method 2 that follows). Method 1
Using the top equation: Replace y with
and solve for x.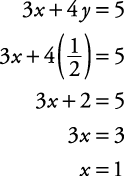 
Method 2
Eliminate y and solve for x.The least common multiple of 4 and 6 is 12. Multiply the top equation by 3 and the bottom equation by 2.
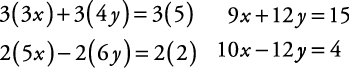
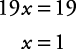
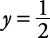. Substitution method
Sometimes a system is more easily solved by the substitution method. This method involves substituting one equation into another.Example 6
Solve for x and y.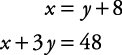
( y + 8) + 3 y = 48
Now solve for y. Simplify by combining y's. 
Check the solution.
Example 7
Solve for x and y using the substitution method.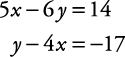
Then proceed as in example 6.
In this example, the bottom equation has a “1” in front of the y.
Solve for y in terms of x.
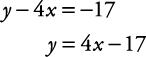
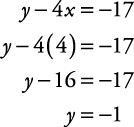
Check the solution:
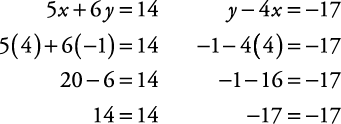
Graphing method
Another method of solving equations is by graphing each equation on a coordinate graph. The coordinates of the intersection will be the solution to the system. If you are unfamiliar with coordinate graphing, carefully review the articles on coordinate geometry before attempting this method.Example 8
Solve the system by graphing.
| x | y |
|---|---|
| 4 | 0 |
| 2 | –2 |
| 5 | 1 |
| x | y |
|---|---|
| 1 | –1 |
| 4 | 0 |
| 7 | 1 |
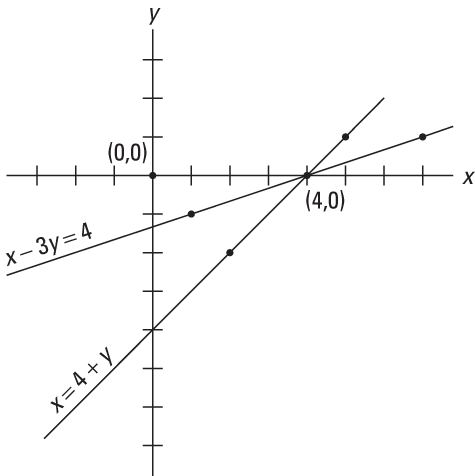
The point where the two lines cross (4, 0) is the solution of the system.
If the lines are parallel, they do not intersect, and therefore, there is no solution to that system.
Figure 1. The graph of lines x = 4 + y and x – 3 y = 4 indicating the solution.
Example 9
Solve the system by graphing.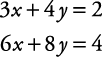
3 x + 4 y = 2 6 x + 8 y = 4
Following are the tables of x and y values. See Figure 2. | x | y |
|---|---|
| 0 |  |
| 2 | – 1 |
| 4 |  |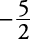
| x | y |
|---|---|
| 0 |  |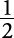
| 2 | – 1 |
| 4 |  |
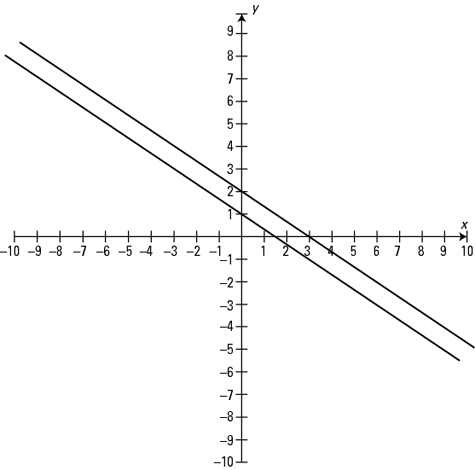
Therefore, the solution is not a unique point. The solution is all the points on the line.
Therefore, the solution is either equation of the line since they both represent the same line.
This is like Example when it was done using the addition/subtraction method.
Figure 2. The graph of lines 3 x + 4 y = 2 and 6 x + 8 y = 4 indicating the solution.
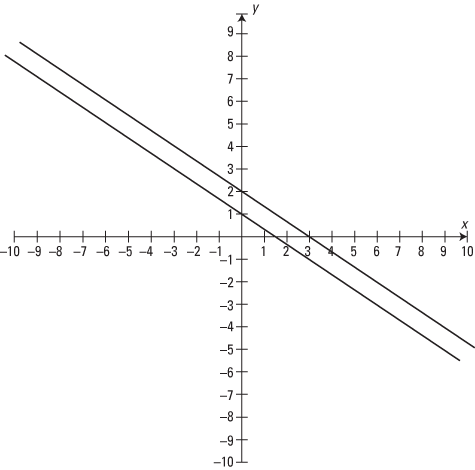
Example 10
Solve the system by graphing.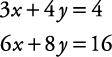
| x | y |
|---|---|
| 0 | 1 |
| 2 |  |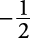
| 4 | –2 |
| x | y |
|---|---|
| 0 | 2 |
| 2 |  |
| 4 | –1 |
No solution exists for this system of equations.
This is like Example done using the addition/subtraction method.
Figure 3. The graph of lines 3 x + 4 y = 4 and 6 x + 8 y = 16, indicating the solution.
