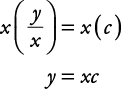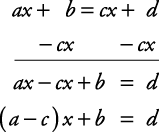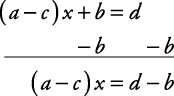Published On:Thursday, 8 December 2011
Posted by Muhammad Atif Saeed
Equations
Equations
An equation is a mathematical sentence, a relationship between numbers and/or symbols that says two expressions are of equal value.Axioms of equality
For all real numbers a, b, and c, the following are some basic rules for using the equal sign.- Reflexive axiom: a = a.
Therefore, 4 = 4. - Symmetric axiom: If a = b, then b = a.
Therefore, if 2 + 3 = 5, then 5 = 2 + 3. - Transitive axiom: If a = b and b = c, then a = c.
Therefore, if 1 + 3 = 4 and 4 = 2 + 2, then 1 + 3 = 2 + 2. - Additive axiom of equality: If a = b and c = d, then a + c = b + d.
Therefore, if 1 + 1 = 2 and 3 + 3 = 6, then 1 + 1 + 3 + 3 = 2 + 6. - Multiplicative axiom of equality: If a = b and c = d, then ac = bd.
Therefore, if 1 = and 4 =
and 4 = 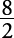 , then
, then 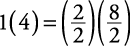 .
.
Solving equations
Remember that an equation is like a balance scale with the equal sign (=) being the fulcrum, or center. Thus, if you do the same thing to each side of the equation (say, add 5 to each side), the equation will still be balanced.Example 1
Solve for x. x – 5 = 23
To solve the equation x – 5 = 23, you must get x by itself on one side; therefore, add 5 to each side of the equation. 
Example 2
Solve for x.3 x + 4 = 19
Subtract 4 from each side of the equation to get the 3 x by itself on one side. 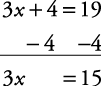

To check, substitute your answer into the original equation.
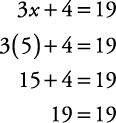
Example 3
Solve for x.
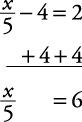

Example 4
Solve for x.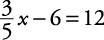
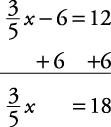
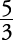 (same as dividing by
(same as dividing by 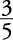 ).
). 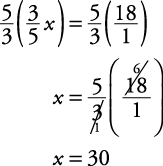
Example 5
Solve for x.5 x = 2 x – 6
Subtract 2 x from each side of the equation. 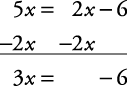

Example 6
Solve for x.6 x + 3 = 4 x + 5
Subtract 4 x from each side of the equation. 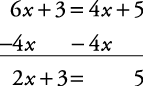

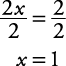
Literal equations
Literal equations have no numbers, only symbols (letters).Example 7
Solve for q. qp – x = y
First add x to each side of the equation. 

Example 8
Solve for y.