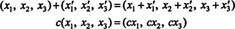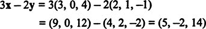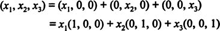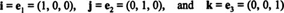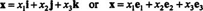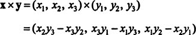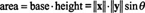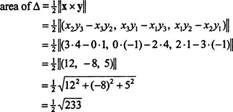The Space R³

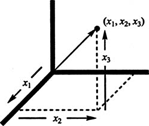
If three mutually perpendicular copies of the real line intersect at their origins, any point in the resulting space is specified by an ordered triple of real numbers ( x₁, x₂, x₃). The set of all ordered triples of real numbers is called 3-space, denoted R³ (“R three”). See Figure 1 .

Figure 1

The operations of addition and scalar multiplication difined on R² carry over to R³:


Vectors in R³ are called 3-vectors (because there are 3 components), and the geometric descriptions of addition and scalar multiplication given for 2-vectors also carry over to 3-vectors.
Example 1: If x = (3, 0, 4) and y = (2, 1, −1), then


Standard basis vectors in R³ . Since for any vector x = ( x₁, x₂, x₃) in R³,


the standard basis vectors in R³ are

Any vector x in R³ may therefore be written as


See Figure 2 .

Figure 2

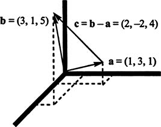
Example 2: What vector must be added to a = (1, 3, 1) to yield b = (3, 1, 5)?
Let c be the required vector; then a + c = b. Therefore,


Note that c is the vector ab; see Figure 3 .

Figure 3

The cross product. So far, you have seen how two vectors can be added (or subtracted) and how a vector is multiplied by a scalar. Is it possible to somehow “multiply” two vectors? One way to define the product of two vectors—which is done only with vectors in R³—is to form their cross product. Let x = ( x₁, x₂, x₃) and y =( y₁, y₂, y₃) be two vectors in R³. The cross product (or vector product) of x and y is defined as follows:


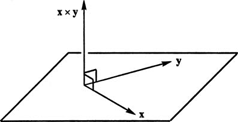
The cross product of two vectors is a vector, and perhaps the most important characteristic of this vector product is that it is perpendicular to both factors. (This will be demonstrated when the dot product is introduced.) That is, the vector x x y will be perpendicular to both x and y; see Figure 4 . [There is an ambiguity here: the plane in Figure 4 , which contains the vectors x and y, has two perpendicular directions: “up” and “down.” Which one does the cross product choose? The answer is given by the right-hand rule: Place the wrist of your right hand at the common initial point of x and y, with your fingers pointing along x; as you curl your fingers toward y, your thumb will point in the direction of x x y. This shows that the cross product is anticommutative: y x x = − ( x x y).]

Figure 4

The length of a vector x = ( x₁, x₂, x₃) in R³, which is denoted ∥ x∥, is given by the equation


a result which follows from the Pythagorean Theorem (see the discussion preceding Figure 7 below). While the direction of the cross product of x and y is determined by orthogonality and the right-hand rule, the magnitude (that is, the length) of x x y is equal to the area of the parallelogram spanned by the vectors x and y. Since the area of the parallelogram in Figure 5 is


the following equation holds:

where θ is the angle between x and y.

Figure 5

Example 3: Let x = (2, 3, 0) and y = (−1, 1, 4) be position vectors in R³. Compute the area of the triangle whose vertices are the origin and the endpoints of x and y and determine the angle between the vectors x and y.
Since the area of the triangle is half the area of the parallelogram spanned by x and y,


Now, since ‖ x x y‖ = ‖ x‖·‖ y‖ sin θ, the angle between x and y is given by


Therefore, θ = sin⁻¹ √233/234.

About the Author

By Muhammad Atif Saeed on 00:07. Filed under Mathandstat . Follow any responses to the RSS 2.0. Leave a response