Published On:Friday, 9 December 2011
Posted by Muhammad Atif Saeed
Linear Equations: Solutions Using Substitution with Two Variables
Linear Equations: Solutions Using Substitution with Two Variables
To solve systems using substitution, follow this procedure:class="numbered">
Usually, when using the substitution method, one equation and one of the variables leads to a quick solution more readily than the other. That's illustrated by the selection of x and the second equation in the following example.
Example 1
Solve this system of equations by using substitution.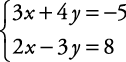
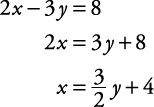
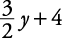for x in the other equation.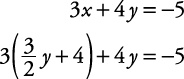 
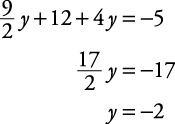
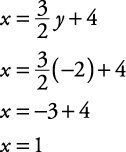
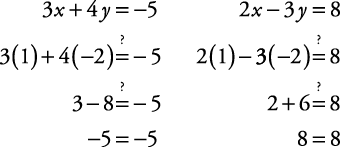
If the substitution method produces a sentence that is always true, such as 0 = 0, then the system is dependent, and either original equation is a solution. If the substitution method produces a sentence that is always false, such as 0 = 5, then the system is inconsistent, and there is no solution.
