Intuitive Definition
The concept of the limit of a function is essential to the study of calculus. It is used in defining some of the most important concepts in calculus—continuity, the derivative of a function, and the definite integral of a function.
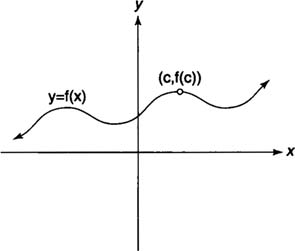
The
limit of a function
f(
x) describes the behavior of the function close to a particular
x value. It does not necessarily give the value of the function at
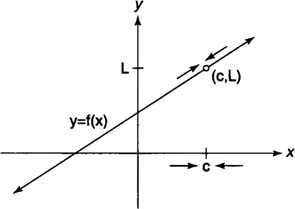
x. You write
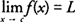
, which means that as
x “approaches”
c, the function
f(
x) “approaches” the real number
L (see Figure
1 ).
|
| |
|
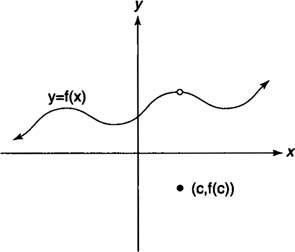
| Figure 1 | The limit of f(x) as x approaches c.
|
|
|
In other words, as the independent variable x gets closer and closer to c, the function value f( x) gets closer to L. Note that this does not imply that f( c) = L; in fact, the function may not even exist at c (Figure 2 ) or may equal some value different than
L at
c (Figure
3 ).
|
| |
|
| Figure 2 | f ( c) does not exist, but 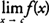 does. does.
|
|
|
|
| |
|
| Figure 3 | f ( c) and 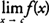 are not equal. are not equal.
|
|
|
If the function does not approach a real number L as x approaches c, the limit does not exist; therefore, you write 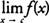 DNE (Does Not Exist). Many different situations could occur in determining that the limit of a function does not exist as x approaches some value.
DNE (Does Not Exist). Many different situations could occur in determining that the limit of a function does not exist as x approaches some value.
About the Author
Posted by Muhammad Atif Saeed
on 01:41. Filed under
Calculus,
Mathandstat
.
You can follow any responses to this entry through the RSS 2.0.
Feel free to leave a response
By Muhammad Atif Saeed
on 01:41. Filed under
Calculus
,
Mathandstat
.
Follow any responses to the RSS 2.0. Leave a response
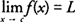 , which means that as x “approaches” c, the function f( x) “approaches” the real number L (see Figure 1 ).
, which means that as x “approaches” c, the function f( x) “approaches” the real number L (see Figure 1 ). 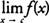 DNE (Does Not Exist). Many different situations could occur in determining that the limit of a function does not exist as x approaches some value.
DNE (Does Not Exist). Many different situations could occur in determining that the limit of a function does not exist as x approaches some value.







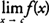 does.
does.