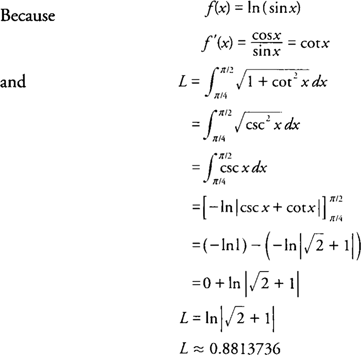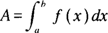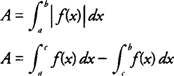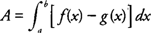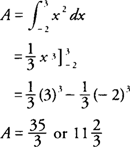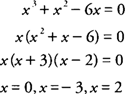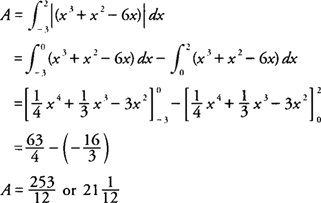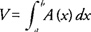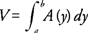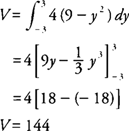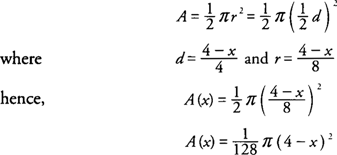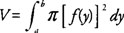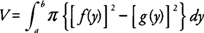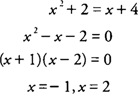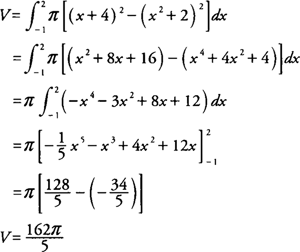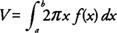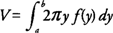Area
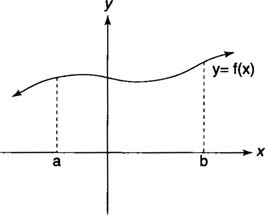
The area of a region bounded by a graph of a function, the
x-axis, and two vertical boundaries can be determined directly by evaluating a definite integral. If
f(x) ≥ 0 on [
a, b], then the area (
A) of the region lying below the graph of
f(x), above the
x-axis, and between the lines
x =
a and
x =
b is
|
| |
|
| Figure 1 | Finding the area under a non-negative function.
|
|
|
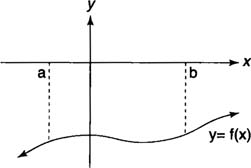
If
f(x) ≤ 0 on [
a, b], then the area (
A) of the region lying above the graph of
f(x), below the
x-axis, and between the lines
x =
a and
x =
b is
|
| |
|
| Figure 2 | Finding the area above a negative function.
|
|
|
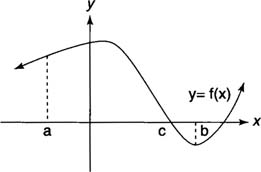
If
f(x) ≥ 0 on [
a, c] and
f(x) ≤ 0 on [
c, b], then the area (
A) of the region bounded by the graph of
f(x), the
x-axis, and the lines
x =
a and
x =
b would be determined by the following definite integrals:
|
| |
|
| Figure 3 | The area bounded by a function whose sign changes.
|
|
|
Note that in this situation it would be necessary to determine all points where the graph
f(x) crosses the
x-axis and the sign of
f(x) on each corresponding interval.
For some problems that ask for the area of regions bounded by the graphs of two or more functions, it is necessary to determined the position of each graph relative to the graphs of the other functions of the region. The points of intersection of the graphs might need to be found in order to identify the limits of integration. As an example, if
f(x) ≥
g(
x) on [
a, b], then the area (
A) of the region between the graphs of
f(x) and
g(
x) and the lines
x =
a and
x =
b is
|
| |
|
| Figure 4 | The area between two functions.
|
|
|
Note that an analogous discussion could be given for areas determined by graphs of functions of
y, the
y-axis, and the lines
y =
a and
y =
b.
Example 1: Find the area of the region bounded by
y =
x2, the
x-axis,
x = –2, and
x = 3.
Because
f(x) ≥ 0 on [–2,3], the area (
A) is
Example 2: Find the area of the region bounded by
y =
x3 +
x2 – 6
x and the
x-axis.
Setting
y = 0 to determine where the graph intersects the
x-axis, you find that
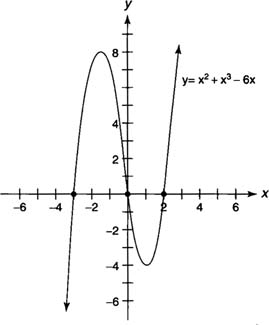
Because f ( x) ≥ 0 on [–3,0] and f ( x) ≤ 0 on [0,2] (see Figure 5 ), the area (
A) of the region is
|
| |
|
| Figure 5 | Diagram for Example 2.
|
|
|
Example 3: Find the area bounded by
y =
x2 and
y = 8 –
x2.
Because
y =
x2 and
y = 8 –
x2, you find that
hence, the curves intersect at (–2,4) and (2,4). Because 8 – x2 ≥ x2 on [–2,2] (see Figure 6 ), the area (
A) of the region is
|
| |
|
| Figure 6 | Diagram for Example 3.
|
|
Volumes of Solids with Known Cross Sections
You can use the definite integral to find the volume of a solid with specific cross sections on an interval, provided you know a formula for the region determined by each cross section. If the cross sections generated are perpendicular to the
x-axis, then their areas will be functions of
x, denoted by
A(x). The volume (
V) of the solid on the interval [
a, b] is
If the cross sections are perpendicular to the
y-axis, then their areas will be functions of
y, denoted by
A(y). In this case, the volume (
V) of the solid on [
a, b] is
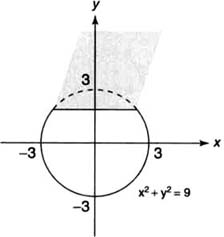
Example 1: Find the volume of the solid whose base is the region inside the circle
x2 +
y2 = 9 if cross sections taken perpendicular to the
y-axis are squares.
Because the cross sections are squares perpendicular to the
y-axis, the area of each cross section should be expressed as a function of
y. The length of the side of the square is determined by two points on the circle
x2 +
y2 = 9 (Figure
1 ).
|
| |
|
| Figure 1 | Diagram for Example 1.
|
|
|
The area ( A) of an arbitrary square cross section is A = s2, where
The volume (
V) of the solid is
Example 2: Find the volume of the solid whose base is the region bounded by the lines
x + 4
y = 4,
x = 0, and
y = 0, if the cross sections taken perpendicular to the
x-axis are semicircles.
Because the cross sections are semicircles perpendicular to the x-axis, the area of each cross section should be expressed as a function of x. The diameter of the semicircle is determined by a point on the line x + 4 y = 4 and a point on the x-axis (Figure 2 ).
|
| |
|
| Figure 2 | Diagram for Example 2.
|
|
|
The area ( A) of an arbitrary semicircle cross section is
The volume (
V) of the solid is
Volumes of Solids of Revolution
You can also use the definite integral to find the volume of a solid that is obtained by revolving a plane region about a horizontal or vertical line that does not pass through the plane. This type of solid will be made up of one of three types of elements—disks, washers, or cylindrical shells—each of which requires a different approach in setting up the definite integral to determine its volume.
Disk method
If the axis of revolution is the boundary of the plane region and the cross sections are taken perpendicular to the axis of revolution, then you use the disk method to find the volume of the solid. Because the cross section of a disk is a circle with area π r2, the volume of each disk is its area times its thickness. If a disk is perpendicular to the x-axis, then its radius should be expressed as a function of x. If a disk is perpendicular to the y-axis, then its radius should be expressed as a function of y.
The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and the x-axis on the interval [ a, b] about the x-axis is
If the region bounded by
x =
f(y) and the
y-axis on [
a, b] is revolved about the
y-axis, then its volume (
V) is
Note that
f(x) and
f(y) represent the radii of the disks or the distance between a point on the curve to the axis of revolution.
Example 1: Find the volume of the solid generated by revolving the region bounded by
y =
x2 and the
x-axis on [−2,3] about the
x-axis.
Because the x-axis is a boundary of the region, you can use the disk method (see Figure 1 ).
|
|
|
| Figure 1 | Diagram for Example 1. |
|
|
The volume ( V) of the solid is
Washer method
If the axis of revolution is not a boundary of the plane region and the cross sections are taken perpendicular to the axis of revolution, you use the washer method to find the volume of the solid. Think of the washer as a “disk with a hole in it” or as a “disk with a disk removed from its center.” If R is the radius of the outer disk and r is the radius of the inner disk, then the area of the washer is π R2 – π r2, and its volume would be its area times its thickness. As noted in the discussion of the disk method, if a washer is perpendicular to the x-axis, then the inner and outer radii should be expressed as functions of x. If a washer is perpendicular to the y-axis, then the radii should be expressed as functions of y.
The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and y = g(x) on the interval [ a, b] where f(x) ≥ g(x), about the x-axis is
If the region bounded by
x =
f(y) and
x =
g(y) on [
a, b], where
f(y) ≥
g(y) is revolved about the
y-axis, then its volume (
V) is
Note again that
f(x) and
g(x) and
f(y) and
g(y) represent the outer and inner radii of the washers or the distance between a point on each curve to the axis of revolution.
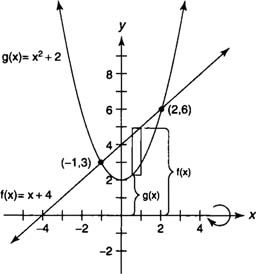
Example 2: Find the volume of the solid generated by revolving the region bounded by
y =
x2 + 2 and
y =
x + 4 about the
x-axis.
Because
y =
x2 + 2 and
y =
x + 4, you find that
The graphs will intersect at (–1,3) and (2,6) with x + 4 ≥ x2 + 2 on [–1,2] (Figure 2 ).
|
|
|
| Figure 2 | Diagram for Example 2. |
|
|
Because the x-axis is not a boundary of the region, you can use the washer method, and the volume ( V) of the solid is
Cylindrical shell method
If the cross sections of the solid are taken parallel to the axis of revolution, then the cylindrical shell method will be used to find the volume of the solid. If the cylindrical shell has radius r and height h, then its volume would be 2π rh times its thickness. Think of the first part of this product, (2π rh), as the area of the rectangle formed by cutting the shell perpendicular to its radius and laying it out flat. If the axis of revolution is vertical, then the radius and height should be expressed in terms of x. If, however, the axis of revolution is horizontal, then the radius and height should be expressed in terms of y.
The volume ( V) of a solid generated by revolving the region bounded by y = f(x) and the x-axis on the interval [ a,b], where f(x) ≥ 0, about the y-axis is
If the region bounded by
x =
f(y) and the
y-axis on the interval [
a,b], where
f(y) ≥ 0, is revolved about the
x-axis, then its volume (
V) is
Note that the
x and
y in the integrands represent the radii of the cylindrical shells or the distance between the cylindrical shell and the axis of revolution. The
f(x) and
f(y) factors represent the heights of the cylindrical shells.
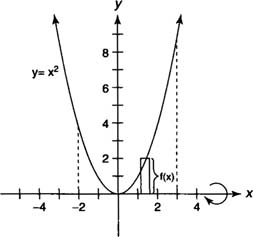
Example 3: Find the volume of the solid generated by revolving the region bounded by
y =
x2 and the
x-axis [1,3] about the
y-axis.
In using the cylindrical shell method, the integral should be expressed in terms of x because the axis of revolution is vertical. The radius of the shell is x, and the height of the shell is f(x) = x2 (Figure 3 ).
|
|
|
| Figure 3 | Diagram for Example 3. |
|
|
The volume ( V) of the solid is
Arc Length
The length of an arc along a portion of a curve is another application of the definite integral. The function and its derivative must both be continuous on the closed interval being considered for such an arc length to be guaranteed. If
y =
f(x) and
y′ =
F'(x) are continuous on the closed interval [
a, b], then the arc length (
L) of
f(x) on [
a,b] is
Similarly, if
x =
f(y) and
x' =
f'(
y) are continuous on the closed interval [
a,b], then the arc length (
L) of
f(y) on [
a,b] is
Example 1: Find the arc length of the graph of
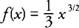
on the interval [0,5].
Example 2: Find the arc length of the graph of
f(x) = ln (sin
x) on the interval [π/4, π/2].

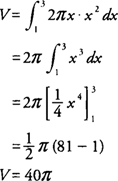
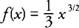 on the interval [0,5].
on the interval [0,5].